变分推断参数化
作者:Madhav Kanda
有时,哈密顿蒙特卡罗 (HMC) 采样器在从后验分布中有效采样时会遇到挑战。一个说明性的例子是 Neal's funnel。在这种情况下,传统的中心化参数化可能不足,需要采用非中心化参数化。然而,在某些情况下,即使非中心化参数化也不够,此时就需要利用变分推断参数化 (Variationally Inferred Parameterization) 来在 0 到 1 的范围内达到所需的中心化。
本教程的目的是使用 Numpyro 中的 LocScaleReparam,基于 概率程序的自动重参数化 来实现变分推断参数化。
[ ]:
%pip -qq install numpyro
%pip -qq install ucimlrepo
[ ]:
import arviz as az
import numpy as np
from ucimlrepo import fetch_ucirepo
import jax
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, SVI, Trace_ELBO
from numpyro.infer.autoguide import AutoDiagonalNormal
from numpyro.infer.reparam import LocScaleReparam
rng_key = jax.random.PRNGKey(0)
1. 数据集
本示例将使用德国信用数据集。该数据集包含 1000 条记录,以及 Hofmann 教授准备的 20 个分类符号属性。在该数据集中,每条记录代表一个在银行获得贷款的人。每个人都根据属性集被归类为良好信用风险或不良信用风险。
[ ]:
def load_german_credit():
statlog_german_credit_data = fetch_ucirepo(id=144)
X = statlog_german_credit_data.data.features
y = statlog_german_credit_data.data.targets
return X, y
[ ]:
X, y = load_german_credit()
X
| 属性1 | 属性2 | 属性3 | 属性4 | 属性5 | 属性6 | 属性7 | 属性8 | 属性9 | 属性10 | 属性11 | 属性12 | 属性13 | 属性14 | 属性15 | 属性16 | 属性17 | 属性18 | 属性19 | 属性20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | A11 | 6 | A34 | A43 | 1169 | A65 | A75 | 4 | A93 | A101 | 4 | A121 | 67 | A143 | A152 | 2 | A173 | 1 | A192 | A201 |
| 1 | A12 | 48 | A32 | A43 | 5951 | A61 | A73 | 2 | A92 | A101 | 2 | A121 | 22 | A143 | A152 | 1 | A173 | 1 | A191 | A201 |
| 2 | A14 | 12 | A34 | A46 | 2096 | A61 | A74 | 2 | A93 | A101 | 3 | A121 | 49 | A143 | A152 | 1 | A172 | 2 | A191 | A201 |
| 3 | A11 | 42 | A32 | A42 | 7882 | A61 | A74 | 2 | A93 | A103 | 4 | A122 | 45 | A143 | A153 | 1 | A173 | 2 | A191 | A201 |
| 4 | A11 | 24 | A33 | A40 | 4870 | A61 | A73 | 3 | A93 | A101 | 4 | A124 | 53 | A143 | A153 | 2 | A173 | 2 | A191 | A201 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 995 | A14 | 12 | A32 | A42 | 1736 | A61 | A74 | 3 | A92 | A101 | 4 | A121 | 31 | A143 | A152 | 1 | A172 | 1 | A191 | A201 |
| 996 | A11 | 30 | A32 | A41 | 3857 | A61 | A73 | 4 | A91 | A101 | 4 | A122 | 40 | A143 | A152 | 1 | A174 | 1 | A192 | A201 |
| 997 | A14 | 12 | A32 | A43 | 804 | A61 | A75 | 4 | A93 | A101 | 4 | A123 | 38 | A143 | A152 | 1 | A173 | 1 | A191 | A201 |
| 998 | A11 | 45 | A32 | A43 | 1845 | A61 | A73 | 4 | A93 | A101 | 4 | A124 | 23 | A143 | A153 | 1 | A173 | 1 | A192 | A201 |
| 999 | A12 | 45 | A34 | A41 | 4576 | A62 | A71 | 3 | A93 | A101 | 4 | A123 | 27 | A143 | A152 | 1 | A173 | 1 | A191 | A201 |
1000 行 × 20 列
这里,X 表示 20 个属性以及数据记录中每个人对应这些属性的值,而 y 是对应这些属性的输出变量。
[ ]:
def data_transform(X, y):
def categorical_to_int(x):
d = {u: i for i, u in enumerate(np.unique(x))}
return np.array([d[i] for i in x])
categoricals = []
numericals = []
numericals.append(np.ones([len(y)]))
for column in X:
column = X[column]
if column.dtype == "O":
categoricals.append(categorical_to_int(column))
else:
numericals.append((column - column.mean()) / column.std())
numericals = np.array(numericals).T
status = np.array(y == 1, dtype=np.int32)
status = np.squeeze(status)
return jnp.array(numericals), jnp.array(categoricals), jnp.array(status)
用于输入到 Numpyro 模型的数据转换
[ ]:
numericals, categoricals, status = data_transform(X, y)
[ ]:
x_numeric = numericals.astype(jnp.float32)
x_categorical = [jnp.eye(c.max() + 1)[c] for c in categoricals]
all_x = jnp.concatenate([x_numeric] + x_categorical, axis=1)
num_features = all_x.shape[1]
y = status[jnp.newaxis, Ellipsis]
2. 模型
我们将使用一个对系数尺度具有分层先验的逻辑回归模型
\begin{align} \log \tau_0 & \sim \mathcal{N}(0,10) & \log \tau_i & \sim \mathcal{N}\left(\log \tau_0, 1\right) \\ \beta_i & \sim \mathcal{N}\left(0, \tau_i\right) & y & \sim \operatorname{Bernoulli}\left(\sigma\left(\beta X^T\right)\right) \end{align}
[ ]:
def german_credit():
log_tau_zero = numpyro.sample("log_tau_zero", dist.Normal(0, 10))
log_tau_i = numpyro.sample(
"log_tau_i", dist.Normal(log_tau_zero, jnp.ones(num_features))
)
beta = numpyro.sample(
"beta", dist.Normal(jnp.zeros(num_features), jnp.exp(log_tau_i))
)
numpyro.sample(
"obs",
dist.Bernoulli(logits=jnp.einsum("nd,md->mn", all_x, beta[jnp.newaxis, :])),
obs=y,
)
[ ]:
nuts_kernel = NUTS(german_credit)
mcmc = MCMC(nuts_kernel, num_warmup=1000, num_samples=1000)
mcmc.run(rng_key, extra_fields=("num_steps",))
sample: 100%|██████████| 2000/2000 [00:21<00:00, 94.07it/s, 63 steps of size 6.31e-02. acc. prob=0.87]
[ ]:
mcmc.print_summary()
mean std median 5.0% 95.0% n_eff r_hat
beta[0] 0.13 0.38 0.05 -0.36 0.74 284.06 1.00
beta[1] -0.34 0.12 -0.34 -0.52 -0.15 621.55 1.00
beta[2] -0.27 0.13 -0.27 -0.45 -0.03 542.13 1.00
beta[3] -0.30 0.10 -0.30 -0.44 -0.11 566.55 1.00
beta[4] -0.00 0.07 -0.00 -0.12 0.11 782.35 1.00
beta[5] 0.12 0.09 0.11 -0.02 0.27 728.28 1.01
beta[6] -0.08 0.08 -0.07 -0.22 0.05 822.89 1.00
beta[7] -0.05 0.07 -0.04 -0.19 0.05 752.66 1.00
beta[8] -0.42 0.32 -0.39 -0.87 0.05 198.00 1.00
beta[9] -0.07 0.26 -0.02 -0.50 0.31 220.27 1.00
beta[10] 0.26 0.31 0.18 -0.15 0.78 404.97 1.00
beta[11] 1.23 0.34 1.25 0.68 1.79 227.34 1.01
beta[12] -0.26 0.34 -0.17 -0.81 0.22 349.10 1.00
beta[13] -0.30 0.34 -0.21 -0.86 0.13 387.72 1.00
beta[14] 0.07 0.20 0.04 -0.26 0.38 240.45 1.03
beta[15] 0.10 0.22 0.05 -0.18 0.50 287.41 1.02
beta[16] 0.76 0.30 0.76 0.22 1.24 364.73 1.03
beta[17] -0.53 0.28 -0.55 -0.94 -0.05 269.95 1.00
beta[18] 0.70 0.42 0.70 -0.02 1.29 367.28 1.00
beta[19] 0.17 0.40 0.06 -0.43 0.77 333.54 1.00
beta[20] 0.03 0.19 0.01 -0.23 0.39 381.57 1.00
beta[21] 0.18 0.22 0.13 -0.14 0.53 335.48 1.00
beta[22] -0.05 0.32 -0.01 -0.56 0.46 439.54 1.00
beta[23] -0.10 0.30 -0.04 -0.63 0.30 508.20 1.00
beta[24] -0.34 0.36 -0.25 -0.94 0.12 283.15 1.00
beta[25] 0.14 0.40 0.04 -0.46 0.71 433.69 1.00
beta[26] -0.01 0.19 -0.00 -0.34 0.28 438.64 1.00
beta[27] -0.36 0.27 -0.33 -0.78 0.04 377.33 1.01
beta[28] -0.07 0.22 -0.03 -0.43 0.26 493.09 1.00
beta[29] 0.01 0.22 0.00 -0.32 0.34 448.21 1.00
beta[30] 0.35 0.43 0.22 -0.18 1.08 314.69 1.00
beta[31] 0.41 0.33 0.40 -0.10 0.90 402.62 1.00
beta[32] -0.03 0.21 -0.01 -0.39 0.30 525.23 1.00
beta[33] -0.12 0.18 -0.09 -0.41 0.16 334.94 1.00
beta[34] -0.02 0.16 -0.01 -0.24 0.26 318.25 1.00
beta[35] 0.42 0.27 0.42 -0.04 0.81 455.99 1.00
beta[36] 0.05 0.17 0.03 -0.18 0.35 506.34 1.00
beta[37] -0.12 0.25 -0.06 -0.57 0.21 470.11 1.00
beta[38] -0.07 0.20 -0.04 -0.39 0.24 410.71 1.00
beta[39] 0.36 0.24 0.35 -0.04 0.71 359.55 1.00
beta[40] 0.05 0.20 0.02 -0.29 0.35 441.70 1.00
beta[41] -0.00 0.21 0.00 -0.34 0.37 513.67 1.00
beta[42] -0.13 0.27 -0.08 -0.59 0.23 402.64 1.00
beta[43] 0.55 0.46 0.49 -0.11 1.28 570.74 1.00
beta[44] 0.19 0.21 0.15 -0.14 0.50 379.76 1.00
beta[45] -0.00 0.16 0.00 -0.25 0.26 352.19 1.00
beta[46] 0.01 0.16 0.01 -0.25 0.25 411.05 1.00
beta[47] -0.16 0.24 -0.11 -0.55 0.18 455.59 1.00
beta[48] -0.12 0.24 -0.07 -0.55 0.21 322.67 1.04
beta[49] -0.04 0.23 -0.02 -0.45 0.30 437.47 1.02
beta[50] 0.38 0.28 0.37 -0.03 0.82 266.19 1.04
beta[51] -0.14 0.22 -0.09 -0.52 0.16 406.31 1.00
beta[52] 0.19 0.23 0.14 -0.14 0.55 338.97 1.00
beta[53] 0.04 0.22 0.02 -0.23 0.43 438.03 1.00
beta[54] 0.05 0.24 0.02 -0.32 0.41 522.43 1.00
beta[55] 0.02 0.14 0.01 -0.22 0.23 562.00 1.00
beta[56] -0.01 0.13 -0.01 -0.24 0.21 638.20 1.00
beta[57] 0.01 0.17 0.00 -0.25 0.34 590.99 1.00
beta[58] -0.07 0.18 -0.04 -0.34 0.23 481.37 1.00
beta[59] 0.13 0.19 0.09 -0.12 0.47 507.56 1.00
beta[60] -0.14 0.33 -0.06 -0.64 0.37 303.00 1.00
beta[61] 0.48 0.56 0.32 -0.18 1.41 438.86 1.00
log_tau_i[0] -1.51 0.95 -1.52 -3.03 0.11 290.78 1.00
log_tau_i[1] -1.07 0.67 -1.11 -2.12 0.03 641.04 1.00
log_tau_i[2] -1.24 0.76 -1.26 -2.47 0.03 666.31 1.00
log_tau_i[3] -1.16 0.65 -1.19 -2.20 -0.10 821.60 1.00
log_tau_i[4] -2.11 0.88 -2.13 -3.50 -0.61 806.15 1.00
log_tau_i[5] -1.71 0.86 -1.68 -3.28 -0.44 697.00 1.00
log_tau_i[6] -1.88 0.84 -1.91 -3.30 -0.58 623.56 1.00
log_tau_i[7] -1.99 0.90 -1.98 -3.51 -0.65 710.21 1.00
log_tau_i[8] -1.00 0.86 -0.96 -2.23 0.52 445.30 1.00
log_tau_i[9] -1.69 0.93 -1.63 -3.17 -0.14 326.33 1.00
log_tau_i[10] -1.41 0.95 -1.35 -2.93 0.19 441.60 1.01
log_tau_i[11] -0.11 0.57 -0.12 -0.97 0.80 539.60 1.00
log_tau_i[12] -1.36 0.96 -1.31 -3.16 0.01 336.11 1.00
log_tau_i[13] -1.30 0.95 -1.26 -2.85 0.28 335.04 1.00
log_tau_i[14] -1.72 0.89 -1.70 -3.05 -0.25 584.38 1.00
log_tau_i[15] -1.65 0.92 -1.63 -3.07 -0.10 345.77 1.03
log_tau_i[16] -0.51 0.65 -0.49 -1.42 0.59 676.64 1.00
log_tau_i[17] -0.84 0.76 -0.76 -2.09 0.34 303.14 1.00
log_tau_i[18] -0.69 0.82 -0.59 -2.03 0.61 359.35 1.00
log_tau_i[19] -1.45 0.99 -1.42 -2.97 0.25 397.18 1.00
log_tau_i[20] -1.75 0.94 -1.73 -3.39 -0.40 617.54 1.00
log_tau_i[21] -1.51 0.88 -1.49 -3.16 -0.27 488.52 1.00
log_tau_i[22] -1.56 0.93 -1.56 -3.06 -0.10 348.20 1.00
log_tau_i[23] -1.58 0.94 -1.57 -3.05 0.02 278.69 1.00
log_tau_i[24] -1.26 1.00 -1.12 -2.91 0.29 205.38 1.00
log_tau_i[25] -1.53 0.95 -1.56 -3.11 0.02 351.09 1.00
log_tau_i[26] -1.73 0.91 -1.74 -3.17 -0.22 492.18 1.00
log_tau_i[27] -1.15 0.89 -1.08 -2.66 0.17 485.34 1.00
log_tau_i[28] -1.69 0.92 -1.65 -3.15 -0.19 425.75 1.00
log_tau_i[29] -1.71 0.99 -1.71 -3.19 0.01 374.58 1.00
log_tau_i[30] -1.24 0.99 -1.20 -2.74 0.50 327.47 1.00
log_tau_i[31] -1.02 0.89 -0.91 -2.40 0.51 587.85 1.00
log_tau_i[32] -1.71 0.94 -1.70 -3.22 -0.11 511.74 1.00
log_tau_i[33] -1.69 0.90 -1.68 -3.13 -0.28 538.65 1.00
log_tau_i[34] -1.82 0.92 -1.81 -3.35 -0.35 423.01 1.00
log_tau_i[35] -1.06 0.82 -1.00 -2.30 0.34 470.50 1.00
log_tau_i[36] -1.79 0.87 -1.76 -3.15 -0.34 527.47 1.00
log_tau_i[37] -1.58 0.95 -1.54 -3.11 0.04 485.52 1.00
log_tau_i[38] -1.71 0.87 -1.65 -3.18 -0.34 482.67 1.00
log_tau_i[39] -1.12 0.85 -1.01 -2.44 0.33 337.59 1.00
log_tau_i[40] -1.76 0.96 -1.73 -3.58 -0.36 533.15 1.00
log_tau_i[41] -1.74 0.94 -1.70 -3.26 -0.22 500.91 1.00
log_tau_i[42] -1.57 0.95 -1.54 -3.04 0.01 499.44 1.00
log_tau_i[43] -0.87 0.93 -0.74 -2.28 0.58 445.98 1.00
log_tau_i[44] -1.52 0.89 -1.45 -2.95 -0.13 442.63 1.00
log_tau_i[45] -1.84 0.94 -1.79 -3.21 -0.09 673.31 1.00
log_tau_i[46] -1.82 0.85 -1.83 -3.26 -0.56 579.66 1.00
log_tau_i[47] -1.54 0.90 -1.51 -3.35 -0.30 428.50 1.00
log_tau_i[48] -1.62 0.89 -1.60 -3.00 -0.15 413.30 1.01
log_tau_i[49] -1.71 0.95 -1.68 -3.23 -0.13 514.04 1.00
log_tau_i[50] -1.12 0.92 -0.99 -2.67 0.38 206.76 1.03
log_tau_i[51] -1.61 0.92 -1.58 -3.07 -0.03 477.41 1.00
log_tau_i[52] -1.54 0.90 -1.49 -2.96 -0.09 459.83 1.00
log_tau_i[53] -1.74 0.92 -1.69 -3.13 -0.14 509.51 1.00
log_tau_i[54] -1.68 0.95 -1.67 -3.07 0.10 477.21 1.00
log_tau_i[55] -1.87 0.97 -1.88 -3.49 -0.35 514.38 1.00
log_tau_i[56] -1.87 0.96 -1.84 -3.23 -0.12 574.80 1.00
log_tau_i[57] -1.77 0.86 -1.72 -3.26 -0.36 646.10 1.00
log_tau_i[58] -1.78 0.92 -1.77 -3.18 -0.15 617.59 1.00
log_tau_i[59] -1.67 0.93 -1.61 -3.19 -0.21 510.74 1.00
log_tau_i[60] -1.50 0.99 -1.44 -3.09 0.08 386.86 1.00
log_tau_i[61] -1.09 1.06 -1.00 -2.79 0.52 421.27 1.00
log_tau_zero -1.49 0.26 -1.49 -1.90 -1.05 169.88 1.00
Number of divergences: 37
从 mcmc.print_summary 可以看出,存在 37 个发散。因此,我们将使用变分推断参数化 (VIP) 来减少这些发散。
[ ]:
data = az.from_numpyro(mcmc)
az.plot_trace(data, compact=True);
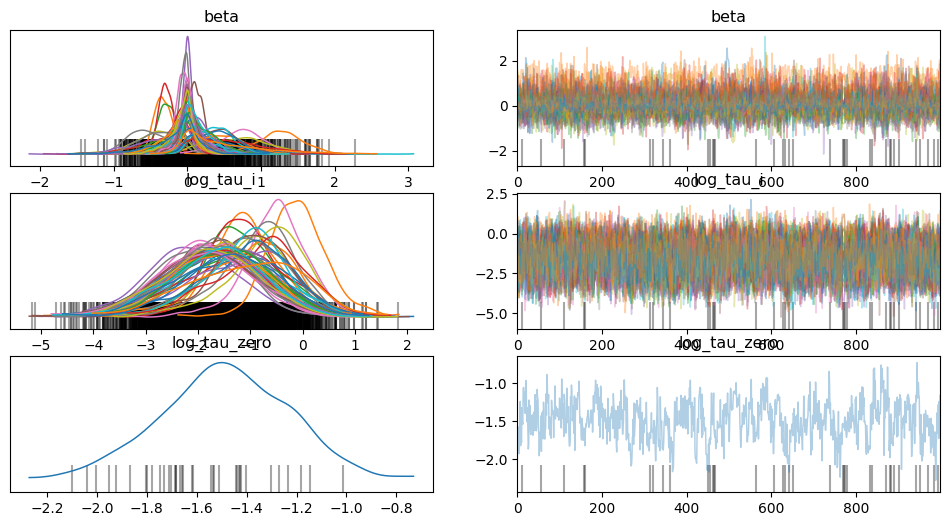
3. 重参数化
我们为任意变量 \(\lambda \in [0,1]\) 引入一个参数化参数 \(z\),并进行变换
=> \(z\) ~ \(N (z | μ, σ)\)
=> 通过定义 \(z\) ~ \(N(λμ, σ^λ)\)
=> \(z\) = \(μ + σ^{1-λ}(z - λμ)\)。
因此,使用上述变换,联合密度可以变换如下: \begin{align} p(\theta, \hat{\mu}, \mathbf{y}) & =\mathcal{N}(\theta \mid 0,1) \times \mathcal{N}\left(\mu \mid \theta, \sigma_\mu\right) \times \mathcal{N}(\mathbf{y} \mid \mu, \sigma) \end{align}
\begin{align} p(\theta, \hat{\mu}, \mathbf{y}) & =\mathcal{N}(\theta \mid 0,1) \times \mathcal{N}\left(\hat{\mu} \mid \lambda \theta, \sigma_\mu^\lambda\right) \times \mathcal{N}\left(\mathbf{y} \mid \theta+\sigma_\mu^{1-\lambda}(\hat{\mu}-\lambda \theta), \sigma\right) \end{align}
[ ]:
def german_credit_reparam(beta_centeredness=None):
def model():
log_tau_zero = numpyro.sample("log_tau_zero", dist.Normal(0, 10))
log_tau_i = numpyro.sample(
"log_tau_i", dist.Normal(log_tau_zero, jnp.ones(num_features))
)
with numpyro.handlers.reparam(
config={"beta": LocScaleReparam(beta_centeredness)}
):
beta = numpyro.sample(
"beta", dist.Normal(jnp.zeros(num_features), jnp.exp(log_tau_i))
)
numpyro.sample(
"obs",
dist.Bernoulli(logits=jnp.einsum("nd,md->mn", all_x, beta[jnp.newaxis, :])),
obs=y,
)
return model
现在,使用 SVI 优化 \(\lambda\)。
[ ]:
model = german_credit_reparam()
guide = AutoDiagonalNormal(model)
svi = SVI(model, guide, numpyro.optim.Adam(3e-4), Trace_ELBO(10))
svi_results = svi.run(rng_key, 10000)
100%|██████████| 10000/10000 [00:16<00:00, 588.87it/s, init loss: 2165.2424, avg. loss [9501-10000]: 576.7846]
[ ]:
reparam_model = german_credit_reparam(
beta_centeredness=svi_results.params["beta_centered"]
)
[ ]:
nuts_kernel = NUTS(reparam_model)
mcmc_reparam = MCMC(nuts_kernel, num_warmup=1000, num_samples=1000)
mcmc_reparam.run(rng_key, extra_fields=("num_steps",))
sample: 100%|██████████| 2000/2000 [00:07<00:00, 285.41it/s, 31 steps of size 1.28e-01. acc. prob=0.89]
[ ]:
mcmc_reparam.print_summary()
mean std median 5.0% 95.0% n_eff r_hat
beta_decentered[0] 0.12 0.40 0.06 -0.48 0.80 338.70 1.00
beta_decentered[1] -0.45 0.15 -0.45 -0.70 -0.21 791.23 1.00
beta_decentered[2] -0.38 0.17 -0.38 -0.65 -0.09 691.79 1.00
beta_decentered[3] -0.41 0.13 -0.41 -0.61 -0.19 1022.79 1.00
beta_decentered[4] -0.01 0.11 -0.01 -0.18 0.20 1176.84 1.00
beta_decentered[5] 0.19 0.14 0.19 -0.04 0.41 1194.41 1.00
beta_decentered[6] -0.13 0.14 -0.13 -0.36 0.09 1227.24 1.00
beta_decentered[7] -0.07 0.12 -0.06 -0.24 0.14 1096.31 1.00
beta_decentered[8] -0.46 0.34 -0.46 -0.99 0.08 330.30 1.00
beta_decentered[9] -0.03 0.32 -0.02 -0.57 0.49 310.35 1.00
beta_decentered[10] 0.35 0.39 0.30 -0.26 1.00 426.11 1.00
beta_decentered[11] 1.29 0.31 1.30 0.81 1.82 433.16 1.00
beta_decentered[12] -0.32 0.39 -0.25 -0.96 0.24 521.05 1.00
beta_decentered[13] -0.38 0.40 -0.32 -1.00 0.24 410.05 1.00
beta_decentered[14] 0.08 0.28 0.06 -0.37 0.57 457.72 1.00
beta_decentered[15] 0.14 0.30 0.10 -0.28 0.66 612.31 1.00
beta_decentered[16] 0.85 0.31 0.86 0.41 1.45 432.14 1.00
beta_decentered[17] -0.64 0.28 -0.65 -1.05 -0.14 523.15 1.00
beta_decentered[18] 0.78 0.42 0.78 0.07 1.46 545.52 1.00
beta_decentered[19] 0.15 0.39 0.08 -0.50 0.80 662.60 1.00
beta_decentered[20] 0.04 0.25 0.03 -0.39 0.40 445.85 1.00
beta_decentered[21] 0.24 0.27 0.21 -0.20 0.65 477.68 1.00
beta_decentered[22] -0.03 0.38 -0.01 -0.64 0.60 984.59 1.00
beta_decentered[23] -0.13 0.34 -0.08 -0.72 0.35 702.87 1.00
beta_decentered[24] -0.41 0.39 -0.37 -1.08 0.13 603.13 1.00
beta_decentered[25] 0.19 0.47 0.09 -0.48 0.92 529.68 1.00
beta_decentered[26] 0.00 0.25 0.01 -0.47 0.35 690.54 1.00
beta_decentered[27] -0.46 0.31 -0.46 -0.95 0.04 464.44 1.00
beta_decentered[28] -0.09 0.30 -0.06 -0.56 0.41 464.65 1.00
beta_decentered[29] 0.02 0.30 0.01 -0.47 0.52 747.44 1.00
beta_decentered[30] 0.38 0.44 0.31 -0.30 1.05 717.12 1.00
beta_decentered[31] 0.47 0.36 0.47 -0.09 1.03 564.18 1.00
beta_decentered[32] -0.03 0.26 -0.02 -0.44 0.44 572.03 1.00
beta_decentered[33] -0.17 0.25 -0.15 -0.63 0.19 713.40 1.00
beta_decentered[34] -0.02 0.21 -0.01 -0.39 0.32 620.45 1.01
beta_decentered[35] 0.53 0.31 0.55 -0.03 1.00 681.60 1.00
beta_decentered[36] 0.09 0.24 0.06 -0.27 0.49 610.06 1.00
beta_decentered[37] -0.14 0.31 -0.10 -0.74 0.28 826.87 1.00
beta_decentered[38] -0.12 0.25 -0.11 -0.53 0.30 493.49 1.00
beta_decentered[39] 0.44 0.28 0.44 -0.01 0.89 542.71 1.00
beta_decentered[40] 0.05 0.26 0.03 -0.39 0.45 709.78 1.00
beta_decentered[41] 0.02 0.30 0.01 -0.52 0.46 389.41 1.00
beta_decentered[42] -0.15 0.33 -0.10 -0.74 0.32 607.05 1.00
beta_decentered[43] 0.66 0.47 0.65 -0.11 1.38 539.31 1.01
beta_decentered[44] 0.25 0.27 0.23 -0.19 0.66 686.63 1.00
beta_decentered[45] -0.01 0.22 -0.00 -0.36 0.35 909.70 1.00
beta_decentered[46] 0.02 0.22 0.01 -0.33 0.39 741.33 1.00
beta_decentered[47] -0.25 0.31 -0.21 -0.72 0.25 487.26 1.00
beta_decentered[48] -0.18 0.30 -0.15 -0.67 0.30 400.57 1.00
beta_decentered[49] -0.07 0.30 -0.05 -0.56 0.41 594.38 1.00
beta_decentered[50] 0.46 0.31 0.46 -0.09 0.88 384.33 1.00
beta_decentered[51] -0.23 0.27 -0.19 -0.69 0.16 561.35 1.00
beta_decentered[52] 0.22 0.25 0.21 -0.19 0.60 456.41 1.00
beta_decentered[53] 0.07 0.29 0.04 -0.41 0.53 500.99 1.00
beta_decentered[54] 0.05 0.30 0.02 -0.49 0.51 896.08 1.00
beta_decentered[55] 0.01 0.23 0.01 -0.34 0.43 1033.13 1.00
beta_decentered[56] -0.02 0.19 -0.01 -0.33 0.28 717.87 1.00
beta_decentered[57] 0.01 0.23 0.01 -0.33 0.41 684.61 1.00
beta_decentered[58] -0.09 0.26 -0.08 -0.55 0.30 455.66 1.01
beta_decentered[59] 0.20 0.27 0.18 -0.20 0.63 413.57 1.01
beta_decentered[60] -0.14 0.37 -0.09 -0.76 0.46 411.83 1.00
beta_decentered[61] 0.58 0.57 0.50 -0.23 1.50 495.86 1.00
log_tau_i[0] -1.56 0.91 -1.53 -2.94 -0.01 480.69 1.00
log_tau_i[1] -1.07 0.64 -1.08 -1.99 0.06 950.02 1.00
log_tau_i[2] -1.25 0.74 -1.23 -2.36 -0.06 796.37 1.00
log_tau_i[3] -1.15 0.65 -1.18 -2.25 -0.14 838.40 1.00
log_tau_i[4] -2.09 0.90 -2.12 -3.51 -0.49 1120.31 1.00
log_tau_i[5] -1.70 0.84 -1.69 -3.10 -0.35 1291.74 1.00
log_tau_i[6] -1.87 0.92 -1.84 -3.67 -0.58 1066.38 1.00
log_tau_i[7] -2.06 0.89 -2.07 -3.42 -0.42 641.48 1.00
log_tau_i[8] -1.11 0.91 -1.03 -2.79 0.19 482.69 1.00
log_tau_i[9] -1.65 0.91 -1.62 -3.05 -0.04 772.73 1.00
log_tau_i[10] -1.31 0.94 -1.27 -2.77 0.24 578.34 1.00
log_tau_i[11] -0.04 0.49 -0.08 -0.81 0.77 736.20 1.00
log_tau_i[12] -1.37 0.98 -1.32 -2.86 0.31 623.14 1.00
log_tau_i[13] -1.28 0.97 -1.21 -2.78 0.30 653.51 1.00
log_tau_i[14] -1.70 0.95 -1.71 -3.20 -0.15 831.88 1.00
log_tau_i[15] -1.67 0.97 -1.65 -3.15 0.04 726.23 1.00
log_tau_i[16] -0.53 0.65 -0.49 -1.55 0.54 558.56 1.00
log_tau_i[17] -0.81 0.68 -0.80 -1.91 0.27 655.36 1.00
log_tau_i[18] -0.71 0.83 -0.60 -1.89 0.75 536.55 1.00
log_tau_i[19] -1.55 0.98 -1.53 -3.17 -0.02 675.27 1.00
log_tau_i[20] -1.81 0.90 -1.79 -3.36 -0.41 823.93 1.00
log_tau_i[21] -1.53 0.93 -1.51 -3.03 -0.04 767.64 1.00
log_tau_i[22] -1.60 0.99 -1.58 -3.25 -0.01 840.71 1.00
log_tau_i[23] -1.64 0.97 -1.60 -3.15 0.10 615.62 1.00
log_tau_i[24] -1.21 0.96 -1.11 -2.61 0.47 674.58 1.00
log_tau_i[25] -1.54 1.04 -1.49 -3.39 -0.01 509.69 1.00
log_tau_i[26] -1.77 0.95 -1.74 -3.27 -0.13 915.91 1.00
log_tau_i[27] -1.14 0.89 -1.07 -2.53 0.36 569.10 1.01
log_tau_i[28] -1.72 0.93 -1.66 -3.25 -0.20 911.70 1.01
log_tau_i[29] -1.70 0.91 -1.71 -3.16 -0.14 648.29 1.00
log_tau_i[30] -1.28 1.02 -1.28 -2.99 0.34 575.90 1.00
log_tau_i[31] -1.10 0.86 -1.04 -2.39 0.45 730.21 1.00
log_tau_i[32] -1.79 0.95 -1.82 -3.32 -0.19 667.95 1.00
log_tau_i[33] -1.64 0.86 -1.62 -3.04 -0.32 948.64 1.00
log_tau_i[34] -1.87 0.92 -1.88 -3.29 -0.25 909.49 1.00
log_tau_i[35] -1.00 0.85 -0.95 -2.44 0.25 672.42 1.00
log_tau_i[36] -1.76 0.92 -1.73 -3.19 -0.22 889.56 1.00
log_tau_i[37] -1.63 1.00 -1.58 -3.11 0.12 973.29 1.00
log_tau_i[38] -1.72 0.85 -1.70 -3.13 -0.30 837.73 1.00
log_tau_i[39] -1.15 0.80 -1.13 -2.32 0.18 627.15 1.00
log_tau_i[40] -1.76 0.93 -1.70 -3.36 -0.34 686.88 1.00
log_tau_i[41] -1.75 0.96 -1.74 -3.20 -0.09 612.83 1.00
log_tau_i[42] -1.62 0.91 -1.62 -3.21 -0.25 596.18 1.00
log_tau_i[43] -0.79 0.93 -0.74 -2.20 0.83 560.52 1.01
log_tau_i[44] -1.52 0.94 -1.48 -3.08 0.01 888.27 1.00
log_tau_i[45] -1.83 0.90 -1.84 -3.27 -0.44 1122.53 1.00
log_tau_i[46] -1.83 0.89 -1.78 -3.21 -0.31 990.03 1.00
log_tau_i[47] -1.56 0.93 -1.48 -3.20 -0.21 736.01 1.00
log_tau_i[48] -1.59 0.94 -1.54 -3.20 -0.01 588.77 1.00
log_tau_i[49] -1.71 0.93 -1.68 -3.17 -0.17 813.94 1.00
log_tau_i[50] -1.15 0.83 -1.11 -2.51 0.14 514.68 1.00
log_tau_i[51] -1.54 0.89 -1.51 -2.97 -0.13 780.67 1.00
log_tau_i[52] -1.59 0.93 -1.56 -3.21 -0.28 807.47 1.00
log_tau_i[53] -1.74 0.92 -1.72 -3.10 -0.15 657.89 1.00
log_tau_i[54] -1.74 0.93 -1.74 -3.09 -0.10 867.29 1.00
log_tau_i[55] -1.89 0.94 -1.87 -3.34 -0.27 1132.90 1.00
log_tau_i[56] -1.89 0.92 -1.89 -3.27 -0.27 980.72 1.00
log_tau_i[57] -1.84 0.91 -1.84 -3.33 -0.38 813.32 1.00
log_tau_i[58] -1.75 0.93 -1.74 -3.25 -0.34 583.52 1.00
log_tau_i[59] -1.59 0.96 -1.53 -3.11 -0.06 754.39 1.01
log_tau_i[60] -1.58 0.98 -1.52 -3.23 -0.08 561.05 1.00
log_tau_i[61] -0.98 1.03 -0.85 -2.55 0.79 502.63 1.00
log_tau_zero -1.49 0.26 -1.49 -1.91 -1.10 220.32 1.00
Number of divergences: 1
发散的数量已从 37 个显著减少到 1 个。
[ ]:
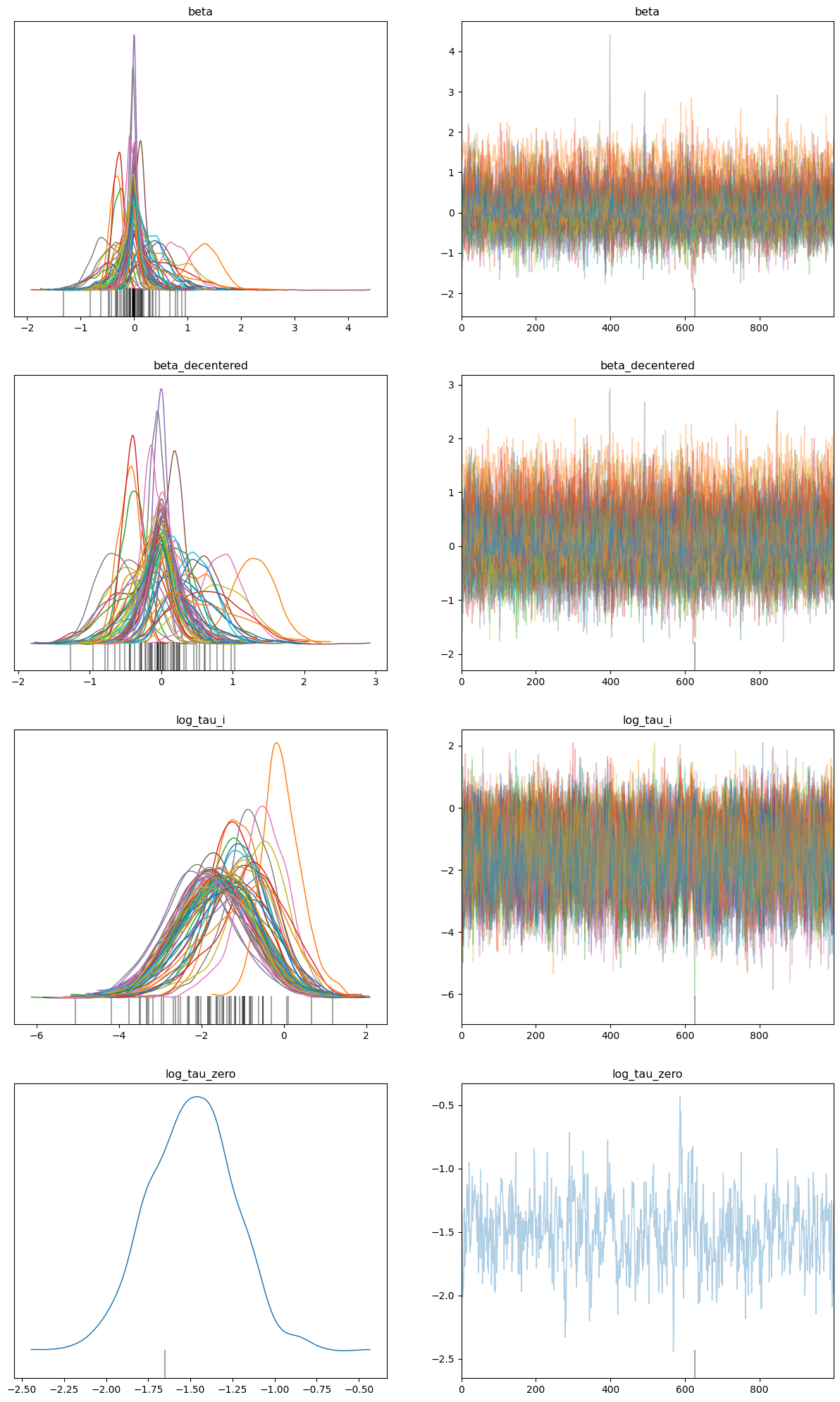
data = az.from_numpyro(mcmc_reparam)
az.plot_trace(data, compact=True, figsize=(15, 25));