交互式在线版本：

使用 NumPyro 进行贝叶斯回归

在本教程中，我们将使用一个改编自《Statistical Rethinking》[1] 的简单示例，探索如何在 NumPyro 中进行贝叶斯回归。特别地，我们希望探索以下内容

使用 NumPyro 原语 sample 编写一个简单模型。
使用 NumPyro 中的 MCMC 运行推断，特别是使用无 U 形采样器 (NUTS) 来获取我们感兴趣的回归参数的后验分布。
了解诸如 Predictive 和 log_likelihood 等推断工具。
了解如何在 NumPyro 中使用效果处理器来生成模型的执行轨迹，根据采样语句进行条件化，使用 RNG 种子对模型进行播种等，并利用这些实现对 MCMC 有用的各种工具。例如，计算模型对数似然，生成后验预测的经验分布等。

[1]:

!pip install -q numpyro@git+https://github.com/pyro-ppl/numpyro

[notice] A new release of pip is available: 24.0 -> 24.2
[notice] To update, run: pip install --upgrade pip

[1]:

import os

from IPython.display import set_matplotlib_formats
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from jax import random, vmap
import jax.numpy as jnp
from jax.scipy.special import logsumexp

import numpyro
from numpyro import handlers
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS

plt.style.use("bmh")
if "NUMPYRO_SPHINXBUILD" in os.environ:
    set_matplotlib_formats("svg")

assert numpyro.__version__.startswith("0.18.0")

数据集

在本例中，我们将使用《Statistical Rethinking》[1] 第 05 章中的 WaffleDivorce 数据集。该数据集包含美国 50 个州的离婚率，以及人口、平均结婚年龄、是否是南方州等预测变量，还有一个奇怪的变量：Waffle House 的数量。

[2]:

DATASET_URL = "https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/WaffleDivorce.csv"
dset = pd.read_csv(DATASET_URL, sep=";")
dset

[2]:

	地点	位置简称	人口	平均结婚年龄	结婚率	结婚率标准误	离婚率	离婚率标准误	Waffle House 数量	南方州	1860 年奴隶数量	1860 年人口数量	1860 年奴隶比例
0	阿拉巴马州	AL	4.78	25.3	20.2	1.27	12.7	0.79	128	1	435080	964201	0.450000
1	阿拉斯加州	AK	0.71	25.2	26.0	2.93	12.5	2.05	0	0	0	0	0.000000
2	亚利桑那州	AZ	6.33	25.8	20.3	0.98	10.8	0.74	18	0	0	0	0.000000
3	阿肯色州	AR	2.92	24.3	26.4	1.70	13.5	1.22	41	1	111115	435450	0.260000
4	加利福尼亚州	CA	37.25	26.8	19.1	0.39	8.0	0.24	0	0	0	379994	0.000000
5	科罗拉多州	CO	5.03	25.7	23.5	1.24	11.6	0.94	11	0	0	34277	0.000000
6	康涅狄格州	CT	3.57	27.6	17.1	1.06	6.7	0.77	0	0	0	460147	0.000000
7	特拉华州	DE	0.90	26.6	23.1	2.89	8.9	1.39	3	0	1798	112216	0.016000
8	哥伦比亚特区	DC	0.60	29.7	17.7	2.53	6.3	1.89	0	0	0	75080	0.000000
9	佛罗里达州	FL	18.80	26.4	17.0	0.58	8.5	0.32	133	1	61745	140424	0.440000
10	佐治亚州	GA	9.69	25.9	22.1	0.81	11.5	0.58	381	1	462198	1057286	0.440000
11	夏威夷州	HI	1.36	26.9	24.9	2.54	8.3	1.27	0	0	0	0	0.000000
12	爱达荷州	ID	1.57	23.2	25.8	1.84	7.7	1.05	0	0	0	0	0.000000
13	伊利诺伊州	IL	12.83	27.0	17.9	0.58	8.0	0.45	2	0	0	1711951	0.000000
14	印第安纳州	IN	6.48	25.7	19.8	0.81	11.0	0.63	17	0	0	1350428	0.000000
15	爱荷华州	IA	3.05	25.4	21.5	1.46	10.2	0.91	0	0	0	674913	0.000000
16	堪萨斯州	KS	2.85	25.0	22.1	1.48	10.6	1.09	6	0	2	107206	0.000019
17	肯塔基州	KY	4.34	24.8	22.2	1.11	12.6	0.75	64	1	225483	1155684	0.000000
18	路易斯安那州	LA	4.53	25.9	20.6	1.19	11.0	0.89	66	1	331726	708002	0.470000
19	缅因州	ME	1.33	26.4	13.5	1.40	13.0	1.48	0	0	0	628279	0.000000
20	马里兰州	MD	5.77	27.3	18.3	1.02	8.8	0.69	11	0	87189	687049	0.130000
21	马萨诸塞州	MA	6.55	28.5	15.8	0.70	7.8	0.52	0	0	0	1231066	0.000000
22	密歇根州	MI	9.88	26.4	16.5	0.69	9.2	0.53	0	0	0	749113	0.000000
23	明尼苏达州	MN	5.30	26.3	15.3	0.77	7.4	0.60	0	0	0	172023	0.000000
24	密西西比州	MS	2.97	25.8	19.3	1.54	11.1	1.01	72	1	436631	791305	0.550000
25	密苏里州	MO	5.99	25.6	18.6	0.81	9.5	0.67	39	1	114931	1182012	0.097000
26	蒙大拿州	MT	0.99	25.7	18.5	2.31	9.1	1.71	0	0	0	0	0.000000
27	内布拉斯加州	NE	1.83	25.4	19.6	1.44	8.8	0.94	0	0	15	28841	0.000520
28	新罕布什尔州	NH	1.32	26.8	16.7	1.76	10.1	1.61	0	0	0	326073	0.000000
29	新泽西州	NJ	8.79	27.7	14.8	0.59	6.1	0.46	0	0	18	672035	0.000027
30	新墨西哥州	NM	2.06	25.8	20.4	1.90	10.2	1.11	2	0	0	93516	0.000000
31	纽约州	NY	19.38	28.4	16.8	0.47	6.6	0.31	0	0	0	3880735	0.000000
32	北卡罗来纳州	NC	9.54	25.7	20.4	0.98	9.9	0.48	142	1	331059	992622	0.330000
33	北达科他州	ND	0.67	25.3	26.7	2.93	8.0	1.44	0	0	0	0	0.000000
34	俄亥俄州	OH	11.54	26.3	16.9	0.61	9.5	0.45	64	0	0	2339511	0.000000
35	俄克拉荷马州	OK	3.75	24.4	23.8	1.29	12.8	1.01	16	0	0	0	0.000000
36	俄勒冈州	OR	3.83	26.0	18.9	1.10	10.4	0.80	0	0	0	52465	0.000000
37	宾夕法尼亚州	PA	12.70	27.1	15.5	0.48	7.7	0.43	11	0	0	2906215	0.000000
38	罗德岛州	RI	1.05	28.2	15.0	2.11	9.4	1.79	0	0	0	174620	0.000000
39	南卡罗来纳州	SC	4.63	26.4	18.1	1.18	8.1	0.70	144	1	402406	703708	0.570000
40	南达科他州	SD	0.81	25.6	20.1	2.64	10.9	2.50	0	0	0	4837	0.000000
41	田纳西州	TN	6.35	25.2	19.4	0.85	11.4	0.75	103	1	275719	1109801	0.200000
42	得克萨斯州	TX	25.15	25.2	21.5	0.61	10.0	0.35	99	1	182566	604215	0.300000
43	犹他州	UT	2.76	23.3	29.6	1.77	10.2	0.93	0	0	0	40273	0.000000
44	佛蒙特州	VT	0.63	26.9	16.4	2.40	9.6	1.87	0	0	0	315098	0.000000
45	弗吉尼亚州	VA	8.00	26.4	20.5	0.83	8.9	0.52	40	1	490865	1219630	0.400000
46	华盛顿州	WA	6.72	25.9	21.4	1.00	10.0	0.65	0	0	0	11594	0.000000
47	西弗吉尼亚州	WV	1.85	25.0	22.2	1.69	10.9	1.34	4	1	18371	376688	0.049000
48	威斯康星州	WI	5.69	26.3	17.2	0.79	8.3	0.57	0	0	0	775881	0.000000
49	怀俄明州	WY	0.56	24.2	30.7	3.92	10.3	1.90	0	0	0	0	0.000000

让我们使用 seaborn.pairplot 绘制数据集中主要变量之间的两两关系。

[9]:

vars = [
    "Population",
    "MedianAgeMarriage",
    "Marriage",
    "WaffleHouses",
    "South",
    "Divorce",
]
sns.pairplot(dset, x_vars=vars, y_vars=vars, palette="husl");

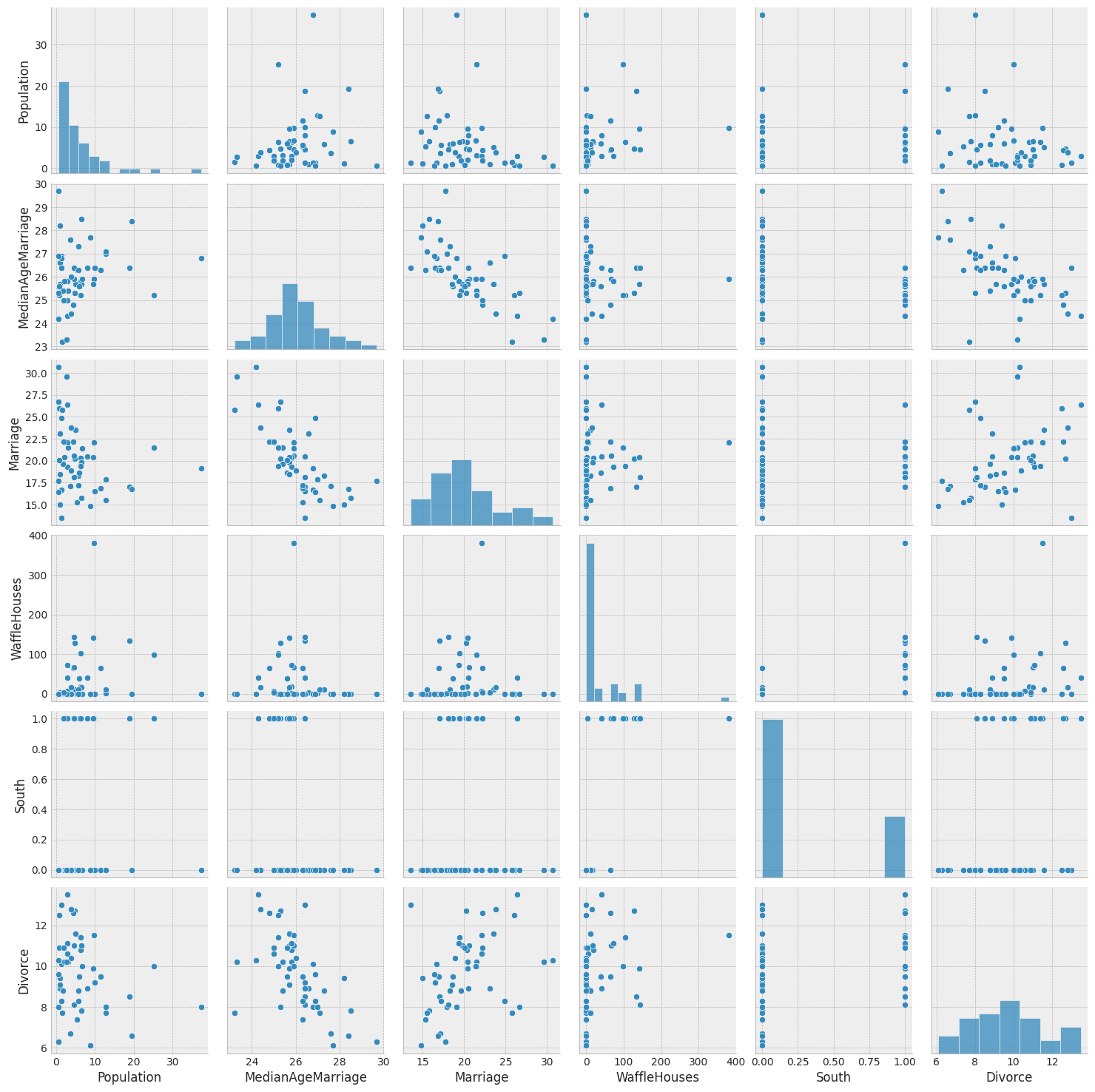
../_images/tutorials_bayesian_regression_6_0.png

从上面的图表中，我们可以清楚地观察到州内的离婚率和结婚率之间存在关联（正如预期），离婚率和平均结婚年龄之间也存在关联。

Waffle House 数量与离婚率之间也存在微弱关联，这从上面的图表中不太明显，但如果我们对 Divorce 与 WaffleHouse 进行回归并绘制结果，则会更清晰。

[5]:

sns.regplot(x="WaffleHouses", y="Divorce", data=dset);

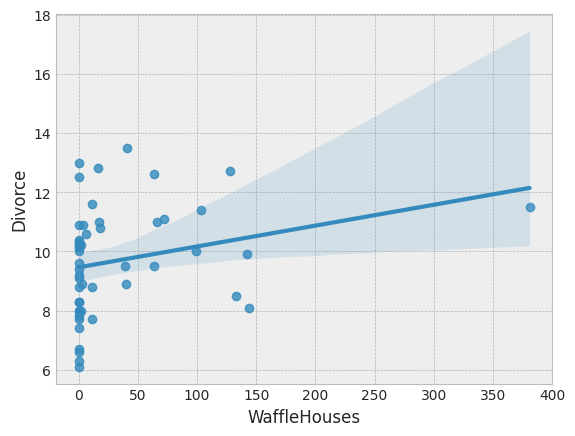
../_images/tutorials_bayesian_regression_8_0.png

这是一个虚假关联的例子。我们不期望一个州的 Waffle House 数量会影响离婚率，但它可能与影响离婚率的其他因素相关。在本教程中，我们不会深入探讨这种虚假关联，但有兴趣的读者可以阅读 [1] 的第 5 章和第 6 章，其中探讨了在存在多个预测变量的情况下因果关联的问题。

为简单起见，在本教程的其余部分，我们将主要关注结婚率和平均结婚年龄作为离婚率的预测变量。

预测离婚率的回归模型

现在让我们在 NumPyro 中编写一个回归模型，将各州的离婚率预测为结婚率和平均结婚年龄的线性函数。

首先，请注意我们的预测变量具有不同的尺度。将预测变量和响应变量标准化到均值 0 和标准差 1 是一个好习惯，这应该会带来更快的推断。

[3]:

def standardize(x):
    return (x - x.mean()) / x.std()


dset["AgeScaled"] = dset.MedianAgeMarriage.pipe(standardize)
dset["MarriageScaled"] = dset.Marriage.pipe(standardize)
dset["DivorceScaled"] = dset.Divorce.pipe(standardize)

我们将 NumPyro 模型编写如下。虽然代码大体上是自解释的，但请注意以下几点

在 NumPyro 中，模型代码是任何可调用的 Python 对象，它可以选择性地接受额外的参数和关键字。对于本教程中使用的 HMC，这些参数和关键字在推断期间保持静态，但我们可以重用相同的模型在新数据上生成预测。
除了常规的 Python 语句外，模型代码还包含诸如 sample 之类的原语。这些原语可以使用效果处理器解释为各种副作用。有关效果处理器的更多信息，请参阅 [3]、[4]。现在，只需记住 sample 语句使得这是一个随机函数，可以从先验分布中采样一些潜变量。我们的目标是根据观测数据推断这些参数的后验分布。
我们将预测变量保留为可选关键字参数的原因是为了能够在改变预测变量集时重用同一个模型。类似地，响应变量之所以是可选的，是因为我们希望重用此模型从后验预测分布中进行采样。请参阅关于绘制后验预测分布的部分，作为一个示例。

[4]:

def model(marriage=None, age=None, divorce=None):
    a = numpyro.sample("a", dist.Normal(0.0, 0.2))
    M, A = 0.0, 0.0
    if marriage is not None:
        bM = numpyro.sample("bM", dist.Normal(0.0, 0.5))
        M = bM * marriage
    if age is not None:
        bA = numpyro.sample("bA", dist.Normal(0.0, 0.5))
        A = bA * age
    sigma = numpyro.sample("sigma", dist.Exponential(1.0))
    mu = a + M + A
    numpyro.sample("obs", dist.Normal(mu, sigma), obs=divorce)

模型 1：预测变量 - 结婚率

我们首先尝试将离婚率建模为仅依赖于一个变量，即结婚率。如上所述，我们可以使用与之前相同的 model 代码，但只传递 marriage 和 divorce 关键字参数的值。我们将使用无 U 形采样器 (NUTS)（有关 NUTS 算法的更多详细信息，请参见 [5]）来对此简单模型运行推断。

NumPyro 中的哈密顿蒙特卡洛 (或 NUTS) 实现接受一个势能函数。这是模型的负对数联合密度。因此，对于我们上面的模型描述，我们需要构建一个函数，该函数在给定参数值时返回势能（或负对数联合密度）。此外，HMC (或 NUTS) 中的 Verlet 积分器返回使用哈密顿动力学在无约束空间中模拟的样本值。因此，具有有界支持的连续变量需要使用双射变换转换为无约束空间。在将这些值返回给用户之前，我们还需要将这些样本转换回其约束支持。幸运的是，这在后台为我们处理好了，在一个方便的类中用于执行MCMC 推断，该类具有以下方法

run(...)：运行预热，调整步长和质量矩阵，并使用预热阶段的样本进行采样。
print_summary()：打印诊断信息，如分位数、有效样本量和 Gelman-Rubin 诊断。
get_samples()：从后验分布获取样本。

注意以下几点

JAX 使用函数式 PRNG。与其他维护全局随机状态的语言/框架不同，在 JAX 中，每次调用采样器都需要一个显式的 PRNGKey。我们将为后续操作拆分我们的初始随机种子，以免意外地重用相同的种子。
我们使用 NUTS 采样器运行推断。要运行普通的 HMC，我们可以改用 HMC 类。

[5]:

# Start from this source of randomness. We will split keys for subsequent operations.
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)

# Run NUTS.
kernel = NUTS(model)
num_samples = 2000
mcmc = MCMC(kernel, num_warmup=1000, num_samples=num_samples)
mcmc.run(
    rng_key_, marriage=dset.MarriageScaled.values, divorce=dset.DivorceScaled.values
)
mcmc.print_summary()
samples_1 = mcmc.get_samples()

sample: 100%|██████████| 3000/3000 [00:05<00:00, 577.68it/s, 5 steps of size 6.75e-01. acc. prob=0.94]

                mean       std    median      5.0%     95.0%     n_eff     r_hat
         a      0.00      0.11     -0.00     -0.19      0.17   1674.85      1.00
        bM      0.35      0.13      0.35      0.14      0.56   1756.94      1.00
     sigma      0.95      0.10      0.94      0.79      1.12   1632.67      1.00

Number of divergences: 0

回归参数的后验分布

我们注意到进度条在运行 NUTS 时为我们提供了关于接受概率、步长和每个样本所采取步数的在线统计数据。特别是，在预热期间，我们调整步长和质量矩阵以达到某个目标接受概率，默认情况下为 0.8。我们成功地在预热阶段调整了步长以达到此目标。

在预热期间，目标是调整超参数，如步长和质量矩阵（HMC 算法对这些超参数非常敏感），并到达典型集（更多详细信息请参见 [6]）。如果模型规范中存在任何问题，第一个迹象将是低接受概率或非常高的步数。我们使用预热阶段结束时的样本为 MCMC 链（由第二个 sample 进度条表示）播种，然后从中生成所需数量的目标分布样本。

在推断结束时，NumPyro 打印每个潜变量的均值、标准差和 90% 置信区间值。请注意，由于我们对预测变量和响应变量进行了标准化，因此截距的均值应为 0，此处可见。它还打印模型中潜变量的其他收敛诊断信息，包括有效样本量和Gelman-Rubin 诊断 (\(\hat{R}\))。这些诊断的值表明链已收敛到目标分布。在我们的例子中，“目标分布”是我们感兴趣的潜变量的后验分布。请注意，对于更复杂的模型，通常值得使用多个链进行验证。最后，samples_1 是一个集合（在我们的例子中是一个 dict，因为 init_samples 是一个 dict），包含模型中每个潜变量的后验分布样本。

为了查看我们的回归拟合情况，让我们使用后验估计的回归参数绘制回归线以及 90% 可信区间 (CI)。请注意，NumPyro 诊断模块中的 hpdi 函数可用于计算 CI。在下面的函数中，请注意从后验收集的样本都沿着主轴。

[9]:

def plot_regression(x, y_mean, y_hpdi):
    # Sort values for plotting by x axis
    idx = jnp.argsort(x)
    marriage = x[idx]
    mean = y_mean[idx]
    hpdi = y_hpdi[:, idx]
    divorce = dset.DivorceScaled.values[idx]

    # Plot
    fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 6))
    ax.plot(marriage, mean)
    ax.plot(marriage, divorce, "o")
    ax.fill_between(marriage, hpdi[0], hpdi[1], alpha=0.3, interpolate=True)
    return ax


# Compute empirical posterior distribution over mu
posterior_mu = (
    jnp.expand_dims(samples_1["a"], -1)
    + jnp.expand_dims(samples_1["bM"], -1) * dset.MarriageScaled.values
)

mean_mu = jnp.mean(posterior_mu, axis=0)
hpdi_mu = hpdi(posterior_mu, 0.9)
ax = plot_regression(dset.MarriageScaled.values, mean_mu, hpdi_mu)
ax.set(
    xlabel="Marriage rate", ylabel="Divorce rate", title="Regression line with 90% CI"
);

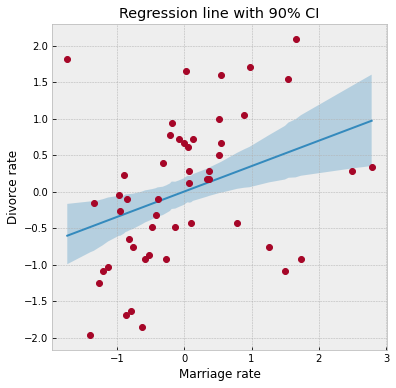
../_images/tutorials_bayesian_regression_17_0.png

从图表中可以看出，CI 在数据相对稀疏的尾部变宽，这正如预期。

先验预测分布

让我们通过从先验预测分布中采样来检查我们是否设置了合理的先验。NumPyro 为此提供了一个方便的预测工具。

[10]:

from numpyro.infer import Predictive

rng_key, rng_key_ = random.split(rng_key)
prior_predictive = Predictive(model, num_samples=100)
prior_predictions = prior_predictive(rng_key_, marriage=dset.MarriageScaled.values)[
    "obs"
]
mean_prior_pred = jnp.mean(prior_predictions, axis=0)
hpdi_prior_pred = hpdi(prior_predictions, 0.9)

ax = plot_regression(dset.MarriageScaled.values, mean_prior_pred, hpdi_prior_pred)
ax.set(xlabel="Marriage rate", ylabel="Divorce rate", title="Predictions with 90% CI");

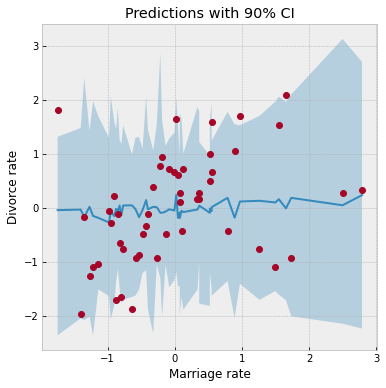
../_images/tutorials_bayesian_regression_19_0.png

请注意，要使 Predictive 按预期工作，模型的响应变量（在此例中为 divorce）必须设置为 None。在上面的代码中，这是通过在调用 prior_predictive 时不向模型传递 divorce 的值来隐式完成的，根据模型定义，这将 divorce 设置为 None。

后验预测分布

现在让我们看看后验预测分布，以了解我们的预测分布与观测到的离婚率相比如何。要从后验预测分布中获取样本，我们需要通过用后验样本替换潜变量来运行模型。请注意，默认情况下，我们为联合后验分布中的每个样本生成一个预测，但这可以使用 num_samples 参数进行控制。

[11]:

rng_key, rng_key_ = random.split(rng_key)
predictive = Predictive(model, samples_1)
predictions = predictive(rng_key_, marriage=dset.MarriageScaled.values)["obs"]
df = dset.filter(["Location"])
df["Mean Predictions"] = jnp.mean(predictions, axis=0)
df.head()

[11]:

	地点	平均预测值
0	阿拉巴马州	0.016434
1	阿拉斯加州	0.501293
2	亚利桑那州	0.025105
3	阿肯色州	0.600058
4	加利福尼亚州	-0.082887

使用效果处理器的预测工具

为了揭开 Predictive 背后的“魔术”，让我们看看如何将效果处理器与 vmap JAX 原语结合起来，实现我们自己的简化预测工具函数，该函数可以进行向量化预测。

[12]:

def predict(rng_key, post_samples, model, *args, **kwargs):
    model = handlers.seed(handlers.condition(model, post_samples), rng_key)
    model_trace = handlers.trace(model).get_trace(*args, **kwargs)
    return model_trace["obs"]["value"]


# vectorize predictions via vmap
predict_fn = vmap(
    lambda rng_key, samples: predict(
        rng_key, samples, model, marriage=dset.MarriageScaled.values
    )
)

请注意在 predict 函数中使用了 condition、seed 和 trace 效果处理器。

seed 效果处理器用于使用初始 PRNGKey 种子包装随机函数。当模型内部调用 sample 语句时，它使用现有种子从分布中采样，但此效果处理器也会拆分现有密钥，以确保模型中未来的 sample 调用使用新拆分的密钥。这样可以避免我们不得不显式地将 PRNGKey 传递给模型中的每个 sample 语句。
condition 效果处理器将潜变量采样点条件化为特定值。在我们的例子中，我们根据 MCMC 返回的后验分布值进行条件化。
trace 效果处理器运行模型并在 OrderedDict 中记录执行轨迹。此轨迹对象包含执行元数据，对于计算对数联合密度等量很有用。

现在应该清楚了，predict 函数只是通过用后验样本（由 mcmc 函数生成）替换潜变量来运行模型以生成预测。请注意使用 JAX 的自动向量化转换 vmap 来向量化预测。请注意，如果我们不使用 vmap，我们将不得不对每个样本使用本地 for 循环，这会慢得多。后验中的每次抽样都可以用于对所有 50 个州进行预测。当我们使用 vmap 对后验中的所有样本进行向量化时，我们将获得一个形状为 (num_samples, 50) 的 predictions_1 数组。然后我们可以计算这些样本的均值和 90% CI 来绘制后验预测分布。我们注意到我们的平均预测值与从 Predictive 工具类获得的值相匹配。

[13]:

# Using the same key as we used for Predictive - note that the results are identical.

predictions_1 = predict_fn(random.split(rng_key_, num_samples), samples_1)

mean_pred = jnp.mean(predictions_1, axis=0)
df = dset.filter(["Location"])
df["Mean Predictions"] = mean_pred
df.head()

[13]:

	地点	平均预测值
0	阿拉巴马州	0.016434
1	阿拉斯加州	0.501293
2	亚利桑那州	0.025105
3	阿肯色州	0.600058
4	加利福尼亚州	-0.082887

[14]:

hpdi_pred = hpdi(predictions_1, 0.9)

ax = plot_regression(dset.MarriageScaled.values, mean_pred, hpdi_pred)
ax.set(xlabel="Marriage rate", ylabel="Divorce rate", title="Predictions with 90% CI");

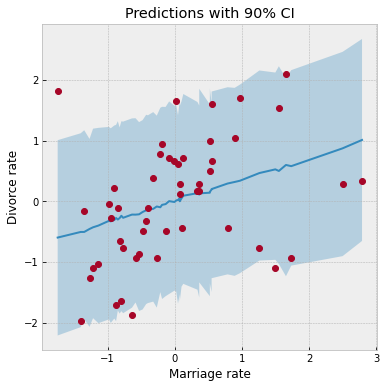
../_images/tutorials_bayesian_regression_27_0.png

我们使用了与之前相同的 plot_regression 函数。我们注意到，由于 sigma 参数引入了额外的噪声，我们预测分布的 CI 比上次绘制的图要宽得多。大多数数据点都在 90% CI 内，这表明拟合良好。

后验预测密度

同样，利用效果处理器和 vmap，我们还可以计算给定数据集的模型对数似然，以及由 [6] 给出的对数后验预测密度：

\[\begin{split} log \prod_{i=1}^{n} \int p(y_i | \theta) p_{post}(\theta) d\theta \approx \sum_{i=1}^n log \frac{\sum_s p(\theta^{s})}{S} \\ = \sum_{i=1}^n (log \sum_s p(\theta^{s}) - log(S))\end{split}\]

.

其中，\(i\) 索引观测数据点 \(y\)，而 \(s\) 索引潜变量 \(\theta\) 的后验样本。如果模型的后验预测密度值相对较高，则表明观测数据点在该模型下具有更高的概率。

[15]:

def log_likelihood(rng_key, params, model, *args, **kwargs):
    model = handlers.condition(model, params)
    model_trace = handlers.trace(model).get_trace(*args, **kwargs)
    obs_node = model_trace["obs"]
    return obs_node["fn"].log_prob(obs_node["value"])


def log_pred_density(rng_key, params, model, *args, **kwargs):
    n = list(params.values())[0].shape[0]
    log_lk_fn = vmap(
        lambda rng_key, params: log_likelihood(rng_key, params, model, *args, **kwargs)
    )
    log_lk_vals = log_lk_fn(random.split(rng_key, n), params)
    return (logsumexp(log_lk_vals, 0) - jnp.log(n)).sum()

请注意，NumPyro 提供了 log_likelihood 工具函数，可直接用于计算任何通用模型的 对数似然，如第一个函数所示。在本教程中，我们希望强调这些工具函数并没有什么神奇之处，您可以使用 NumPyro 的效果处理堆栈来实现自己的推断工具。

[16]:

rng_key, rng_key_ = random.split(rng_key)
print(
    "Log posterior predictive density: {}".format(
        log_pred_density(
            rng_key_,
            samples_1,
            model,
            marriage=dset.MarriageScaled.values,
            divorce=dset.DivorceScaled.values,
        )
    )
)

Log posterior predictive density: -66.70008087158203

模型 2：预测变量 - 平均结婚年龄

现在我们将离婚率建模为平均结婚年龄的函数。计算过程大体上是模型 1 的重复。请注意以下几点

离婚率与结婚年龄呈负相关。因此，平均结婚年龄较低的州很可能离婚率较高。
与模型 1 相比，我们获得了更高的对数似然，这表明平均结婚年龄可能是离婚率更好的预测变量。

[17]:

rng_key, rng_key_ = random.split(rng_key)

mcmc.run(rng_key_, age=dset.AgeScaled.values, divorce=dset.DivorceScaled.values)
mcmc.print_summary()
samples_2 = mcmc.get_samples()

sample: 100%|██████████| 3000/3000 [00:04<00:00, 722.23it/s, 7 steps of size 7.58e-01. acc. prob=0.92]

                mean       std    median      5.0%     95.0%     n_eff     r_hat
         a     -0.00      0.10     -0.00     -0.17      0.16   1942.82      1.00
        bA     -0.57      0.12     -0.57     -0.75     -0.38   1995.70      1.00
     sigma      0.82      0.08      0.82      0.69      0.96   1865.82      1.00

Number of divergences: 0

[18]:

posterior_mu = (
    jnp.expand_dims(samples_2["a"], -1)
    + jnp.expand_dims(samples_2["bA"], -1) * dset.AgeScaled.values
)
mean_mu = jnp.mean(posterior_mu, axis=0)
hpdi_mu = hpdi(posterior_mu, 0.9)
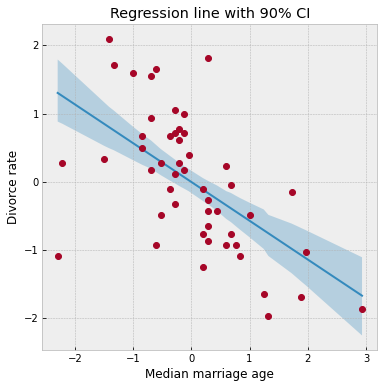
ax = plot_regression(dset.AgeScaled.values, mean_mu, hpdi_mu)
ax.set(
    xlabel="Median marriage age",
    ylabel="Divorce rate",
    title="Regression line with 90% CI",
);

../_images/tutorials_bayesian_regression_34_0.png

[19]:

rng_key, rng_key_ = random.split(rng_key)
predictions_2 = Predictive(model, samples_2)(rng_key_, age=dset.AgeScaled.values)["obs"]

mean_pred = jnp.mean(predictions_2, axis=0)
hpdi_pred = hpdi(predictions_2, 0.9)

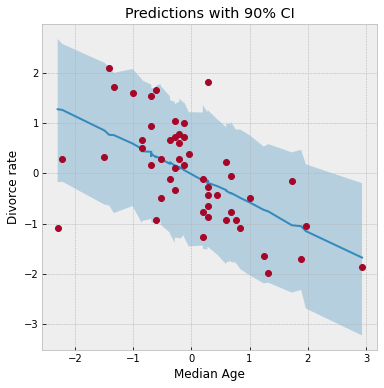
ax = plot_regression(dset.AgeScaled.values, mean_pred, hpdi_pred)
ax.set(xlabel="Median Age", ylabel="Divorce rate", title="Predictions with 90% CI");

../_images/tutorials_bayesian_regression_35_0.png

[20]:

rng_key, rng_key_ = random.split(rng_key)
print(
    "Log posterior predictive density: {}".format(
        log_pred_density(
            rng_key_,
            samples_2,
            model,
            age=dset.AgeScaled.values,
            divorce=dset.DivorceScaled.values,
        )
    )
)

Log posterior predictive density: -59.251956939697266

模型 3：预测变量 - 结婚率和平均结婚年龄

最后，我们还将离婚率建模为依赖于结婚率和平均结婚年龄。请注意，模型的后验预测密度与模型 2 相似，这可能表明在已知平均结婚年龄的情况下，结婚率在预测离婚率方面的边际信息较低。

[21]:

rng_key, rng_key_ = random.split(rng_key)

mcmc.run(
    rng_key_,
    marriage=dset.MarriageScaled.values,
    age=dset.AgeScaled.values,
    divorce=dset.DivorceScaled.values,
)
mcmc.print_summary()
samples_3 = mcmc.get_samples()

sample: 100%|██████████| 3000/3000 [00:04<00:00, 644.48it/s, 7 steps of size 4.65e-01. acc. prob=0.94]

                mean       std    median      5.0%     95.0%     n_eff     r_hat
         a      0.00      0.10      0.00     -0.17      0.16   2007.41      1.00
        bA     -0.61      0.16     -0.61     -0.89     -0.37   1225.02      1.00
        bM     -0.07      0.16     -0.07     -0.34      0.19   1275.37      1.00
     sigma      0.83      0.08      0.82      0.69      0.96   1820.77      1.00

Number of divergences: 0

[22]:

rng_key, rng_key_ = random.split(rng_key)
print(
    "Log posterior predictive density: {}".format(
        log_pred_density(
            rng_key_,
            samples_3,
            model,
            marriage=dset.MarriageScaled.values,
            age=dset.AgeScaled.values,
            divorce=dset.DivorceScaled.values,
        )
    )
)

Log posterior predictive density: -59.06374740600586

各州的离婚率残差

上面的回归图显示，许多州的观测离婚率与平均回归线存在相当大的差异。为了更深入地了解最后一个模型（模型 3）对各州的预测不足或过度预测情况，我们将绘制后验预测以及各州的残差（观测离婚率 - 预测离婚率）。

[23]:

# Predictions for Model 3.
rng_key, rng_key_ = random.split(rng_key)
predictions_3 = Predictive(model, samples_3)(
    rng_key_, marriage=dset.MarriageScaled.values, age=dset.AgeScaled.values
)["obs"]
y = jnp.arange(50)


fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 16))
pred_mean = jnp.mean(predictions_3, axis=0)
pred_hpdi = hpdi(predictions_3, 0.9)
residuals_3 = dset.DivorceScaled.values - predictions_3
residuals_mean = jnp.mean(residuals_3, axis=0)
residuals_hpdi = hpdi(residuals_3, 0.9)
idx = jnp.argsort(residuals_mean)

# Plot posterior predictive
ax[0].plot(jnp.zeros(50), y, "--")
ax[0].errorbar(
    pred_mean[idx],
    y,
    xerr=pred_hpdi[1, idx] - pred_mean[idx],
    marker="o",
    ms=5,
    mew=4,
    ls="none",
    alpha=0.8,
)
ax[0].plot(dset.DivorceScaled.values[idx], y, marker="o", ls="none", color="gray")
ax[0].set(
    xlabel="Posterior Predictive (red) vs. Actuals (gray)",
    ylabel="State",
    title="Posterior Predictive with 90% CI",
)
ax[0].set_yticks(y)
ax[0].set_yticklabels(dset.Loc.values[idx], fontsize=10)

# Plot residuals
residuals_3 = dset.DivorceScaled.values - predictions_3
residuals_mean = jnp.mean(residuals_3, axis=0)
residuals_hpdi = hpdi(residuals_3, 0.9)
err = residuals_hpdi[1] - residuals_mean

ax[1].plot(jnp.zeros(50), y, "--")
ax[1].errorbar(
    residuals_mean[idx], y, xerr=err[idx], marker="o", ms=5, mew=4, ls="none", alpha=0.8
)
ax[1].set(xlabel="Residuals", ylabel="State", title="Residuals with 90% CI")
ax[1].set_yticks(y)
ax[1].set_yticklabels(dset.Loc.values[idx], fontsize=10);

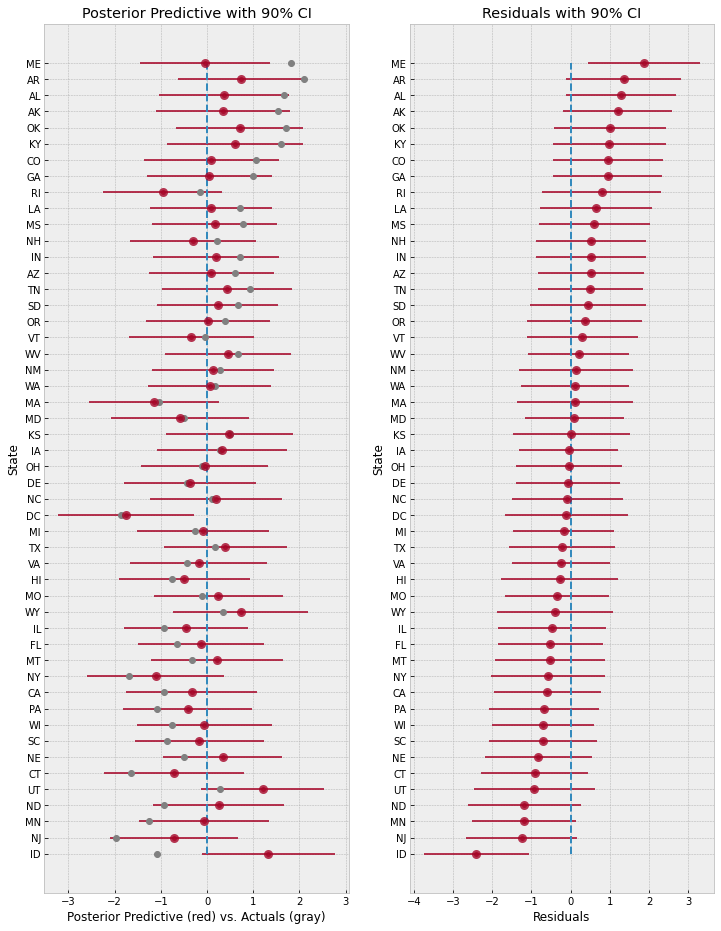
../_images/tutorials_bayesian_regression_41_0.png

左图显示了使用模型 3 对各州进行的平均预测及其 90% CI。灰色标记表示实际观测到的离婚率。右图显示了各州的残差，这两个图都按残差排序，即底部是模型预测值高于观测值的州，而顶部则相反。

总体而言，模型拟合看起来不错，因为大多数观测数据点都在平均预测值周围的 90% CI 内。然而，请注意模型如何大幅过度预测爱达荷州（左下）等州，而在另一端又低估了缅因州（右上）等州。这可能表明我们的模型遗漏了影响不同州离婚率的其他因素。即使忽略其他社会政治变量，我们尚未建模的一个因素是数据集中由 Divorce SE 给出的测量噪声。我们将在下一节中探讨这一点。

含测量误差的回归模型

请注意，在我们之前的模型中，每个数据点对回归线的影响是相同的。这是否合理？我们将以前面的模型为基础，纳入数据集中由 Divorce SE 变量给出的测量误差。纳入测量噪声有助于确保置信度更高（即测量噪声较低）的观测值对回归线有更大影响。另一方面，这也有助于我们更好地建模具有高测量误差的离群值。有关测量噪声导致的误差建模的更多详细信息，请参阅 [1] 的第 14 章。

为此，我们将重用模型 3，唯一的改变是最终观测值具有由 divorce_sd 给出的测量误差（注意这必须是标准化的，因为 divorce 变量本身已标准化为均值 0 和标准差 1）。

[24]:

def model_se(marriage, age, divorce_sd, divorce=None):
    a = numpyro.sample("a", dist.Normal(0.0, 0.2))
    bM = numpyro.sample("bM", dist.Normal(0.0, 0.5))
    M = bM * marriage
    bA = numpyro.sample("bA", dist.Normal(0.0, 0.5))
    A = bA * age
    sigma = numpyro.sample("sigma", dist.Exponential(1.0))
    mu = a + M + A
    divorce_rate = numpyro.sample("divorce_rate", dist.Normal(mu, sigma))
    numpyro.sample("obs", dist.Normal(divorce_rate, divorce_sd), obs=divorce)

[25]:

# Standardize
dset["DivorceScaledSD"] = dset["Divorce SE"] / jnp.std(dset.Divorce.values)

[26]:

rng_key, rng_key_ = random.split(rng_key)

kernel = NUTS(model_se, target_accept_prob=0.9)
mcmc = MCMC(kernel, num_warmup=1000, num_samples=3000)
mcmc.run(
    rng_key_,
    marriage=dset.MarriageScaled.values,
    age=dset.AgeScaled.values,
    divorce_sd=dset.DivorceScaledSD.values,
    divorce=dset.DivorceScaled.values,
)
mcmc.print_summary()
samples_4 = mcmc.get_samples()

sample: 100%|██████████| 4000/4000 [00:06<00:00, 578.19it/s, 15 steps of size 2.58e-01. acc. prob=0.93]

                      mean       std    median      5.0%     95.0%     n_eff     r_hat
               a     -0.06      0.10     -0.06     -0.20      0.11   3203.01      1.00
              bA     -0.61      0.16     -0.61     -0.87     -0.35   2156.51      1.00
              bM      0.06      0.17      0.06     -0.21      0.33   1943.15      1.00
 divorce_rate[0]      1.16      0.36      1.15      0.53      1.72   2488.98      1.00
 divorce_rate[1]      0.69      0.55      0.68     -0.15      1.65   4832.63      1.00
 divorce_rate[2]      0.42      0.34      0.42     -0.16      0.96   4419.13      1.00
 divorce_rate[3]      1.41      0.46      1.40      0.63      2.11   4782.86      1.00
 divorce_rate[4]     -0.90      0.13     -0.90     -1.12     -0.71   4269.33      1.00
 divorce_rate[5]      0.65      0.39      0.65      0.01      1.31   4139.51      1.00
 divorce_rate[6]     -1.36      0.35     -1.36     -1.96     -0.82   5180.21      1.00
 divorce_rate[7]     -0.33      0.49     -0.33     -1.15      0.45   4089.39      1.00
 divorce_rate[8]     -1.88      0.59     -1.88     -2.89     -0.93   3305.68      1.00
 divorce_rate[9]     -0.62      0.17     -0.61     -0.90     -0.34   4936.95      1.00
divorce_rate[10]      0.76      0.29      0.76      0.28      1.24   3627.89      1.00
divorce_rate[11]     -0.55      0.50     -0.55     -1.38      0.26   3822.80      1.00
divorce_rate[12]      0.20      0.53      0.20     -0.74      0.99   1476.70      1.00
divorce_rate[13]     -0.86      0.23     -0.87     -1.24     -0.48   5333.10      1.00
divorce_rate[14]      0.55      0.30      0.55      0.09      1.05   5533.56      1.00
divorce_rate[15]      0.28      0.38      0.28     -0.35      0.92   5179.68      1.00
divorce_rate[16]      0.49      0.43      0.49     -0.23      1.16   5134.56      1.00
divorce_rate[17]      1.25      0.35      1.24      0.69      1.84   4571.21      1.00
divorce_rate[18]      0.42      0.38      0.41     -0.15      1.10   4946.86      1.00
divorce_rate[19]      0.38      0.55      0.36     -0.50      1.29   2145.11      1.00
divorce_rate[20]     -0.56      0.34     -0.56     -1.12     -0.02   5219.59      1.00
divorce_rate[21]     -1.11      0.27     -1.11     -1.53     -0.65   3778.88      1.00
divorce_rate[22]     -0.28      0.26     -0.28     -0.71      0.13   5751.65      1.00
divorce_rate[23]     -0.99      0.30     -0.99     -1.46     -0.49   4385.57      1.00
divorce_rate[24]      0.43      0.41      0.42     -0.26      1.08   3868.84      1.00
divorce_rate[25]     -0.03      0.32     -0.03     -0.57      0.48   5927.41      1.00
divorce_rate[26]     -0.01      0.49     -0.01     -0.79      0.81   4581.29      1.00
divorce_rate[27]     -0.16      0.39     -0.15     -0.79      0.49   4522.45      1.00
divorce_rate[28]     -0.27      0.50     -0.29     -1.08      0.53   3824.97      1.00
divorce_rate[29]     -1.79      0.24     -1.78     -2.18     -1.39   5134.14      1.00
divorce_rate[30]      0.17      0.42      0.16     -0.55      0.82   5978.21      1.00
divorce_rate[31]     -1.66      0.16     -1.66     -1.93     -1.41   5976.18      1.00
divorce_rate[32]      0.12      0.25      0.12     -0.27      0.52   5759.99      1.00
divorce_rate[33]     -0.04      0.52     -0.04     -0.91      0.82   2926.68      1.00
divorce_rate[34]     -0.13      0.22     -0.13     -0.50      0.23   4390.05      1.00
divorce_rate[35]      1.27      0.43      1.27      0.53      1.94   4659.54      1.00
divorce_rate[36]      0.22      0.36      0.22     -0.36      0.84   3758.16      1.00
divorce_rate[37]     -1.02      0.23     -1.02     -1.38     -0.64   5954.84      1.00
divorce_rate[38]     -0.93      0.54     -0.94     -1.84     -0.06   3289.66      1.00
divorce_rate[39]     -0.67      0.33     -0.67     -1.18     -0.09   4787.55      1.00
divorce_rate[40]      0.25      0.55      0.24     -0.67      1.16   4526.98      1.00
divorce_rate[41]      0.73      0.34      0.73      0.17      1.29   4237.28      1.00
divorce_rate[42]      0.20      0.18      0.20     -0.10      0.48   5156.91      1.00
divorce_rate[43]      0.81      0.43      0.81      0.14      1.50   2067.24      1.00
divorce_rate[44]     -0.42      0.51     -0.43     -1.23      0.45   3844.29      1.00
divorce_rate[45]     -0.39      0.25     -0.39     -0.78      0.04   4611.94      1.00
divorce_rate[46]      0.13      0.31      0.13     -0.36      0.64   5879.70      1.00
divorce_rate[47]      0.56      0.47      0.56     -0.15      1.37   4319.38      1.00
divorce_rate[48]     -0.63      0.28     -0.63     -1.11     -0.18   5820.05      1.00
divorce_rate[49]      0.86      0.59      0.88     -0.10      1.79   2460.53      1.00
           sigma      0.58      0.11      0.57      0.40      0.76    735.02      1.00

Number of divergences: 0

纳入测量噪声对残差的影响

请注意，我们的回归系数的值与模型 3 非常相似。然而，引入测量噪声使我们能够更紧密地匹配预测分布与观测值。如果我们像之前一样绘制残差，就可以看到这一点。

[27]:

rng_key, rng_key_ = random.split(rng_key)
predictions_4 = Predictive(model_se, samples_4)(
    rng_key_,
    marriage=dset.MarriageScaled.values,
    age=dset.AgeScaled.values,
    divorce_sd=dset.DivorceScaledSD.values,
)["obs"]

[28]:

sd = dset.DivorceScaledSD.values
residuals_4 = dset.DivorceScaled.values - predictions_4
residuals_mean = jnp.mean(residuals_4, axis=0)
residuals_hpdi = hpdi(residuals_4, 0.9)
err = residuals_hpdi[1] - residuals_mean
idx = jnp.argsort(residuals_mean)
y = jnp.arange(50)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 16))


# Plot Residuals
ax.plot(jnp.zeros(50), y, "--")
ax.errorbar(
    residuals_mean[idx], y, xerr=err[idx], marker="o", ms=5, mew=4, ls="none", alpha=0.8
)

# Plot SD
ax.errorbar(residuals_mean[idx], y, xerr=sd[idx], ls="none", color="orange", alpha=0.9)

# Plot earlier mean residual
ax.plot(
    jnp.mean(dset.DivorceScaled.values - predictions_3, 0)[idx],
    y,
    ls="none",
    marker="o",
    ms=6,
    color="black",
    alpha=0.6,
)

ax.set(xlabel="Residuals", ylabel="State", title="Residuals with 90% CI")
ax.set_yticks(y)
ax.set_yticklabels(dset.Loc.values[idx], fontsize=10)
ax.text(
    -2.8,
    -7,
    "Residuals (with error-bars) from current model (in red). "
    "Black marker \nshows residuals from the previous model (Model 3). "
    "Measurement \nerror is indicated by orange bar.",
);

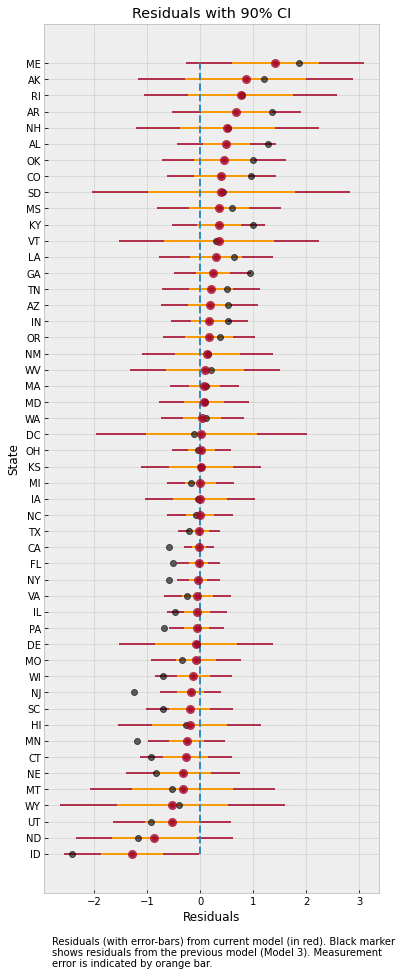
../_images/tutorials_bayesian_regression_49_0.png

上图显示了各州的残差以及由内误差条表示的测量噪声。灰色点是我们之前模型 3 的平均残差。请注意，增加了建模测量噪声的自由度如何缩小了残差。特别是对于爱达荷州和缅因州，在模型中纳入测量噪声后，我们的预测值现在更接近观测值了。

为了更好地了解测量噪声如何影响回归线的移动，让我们绘制残差与测量噪声的关系图。

[29]:

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(10, 6))
x = dset.DivorceScaledSD.values
y1 = jnp.mean(residuals_3, 0)
y2 = jnp.mean(residuals_4, 0)
ax.plot(x, y1, ls="none", marker="o")
ax.plot(x, y2, ls="none", marker="o")
for i, (j, k) in enumerate(zip(y1, y2)):
    ax.plot([x[i], x[i]], [j, k], "--", color="gray")

ax.set(
    xlabel="Measurement Noise",
    ylabel="Residual",
    title="Mean residuals (Model 4: red, Model 3: blue)",
);

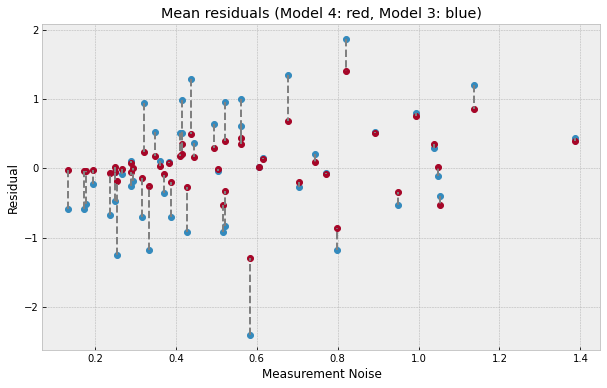
../_images/tutorials_bayesian_regression_51_0.png

上图更详细地展示了发生的情况——回归线本身已经移动，以确保更好地拟合测量噪声较低的观测值（图的左侧），这些观测值的残差已收缩到非常接近 0。也就是说，测量误差较低的数据点在确定回归线时具有相应更高的贡献。另一方面，对于测量误差较高的州（图的右侧），纳入测量噪声使我们能够将后验分布质量更接近观测值，从而也导致残差缩小。

记录 NUTS 使用的梯度评估次数

哈密顿蒙特卡洛（以及扩展的 NUTS）通过计算势函数（表示一组参数产生数据的可能性有多低）并在蒙特卡洛运行过程中重复评估此势函数的梯度来工作。在大多数情况下，此梯度的评估是算法中最昂贵的部分（到目前为止），因此了解此梯度评估了多少次非常有用。这可以通过在调用 mcmc.run 时设置 extra_fields="num_steps" 来完成。

为了计算预热阶段使用的梯度评估次数，我们还必须在调用 mcmc.warmup 时设置 collect_warmup=True。

[18]:

rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)

# Run NUTS.
kernel = NUTS(model)
num_samples = 2000
mcmc = MCMC(kernel, num_warmup=1000, num_samples=num_samples)

# First do the warmup, so we count the number of warmup steps as well.
# Do not forget to set `collect_warmup=True`!
mcmc.warmup(
    rng_key_,
    marriage=dset.MarriageScaled.values,
    divorce=dset.DivorceScaled.values,
    collect_warmup=True,
    extra_fields=("num_steps",),
)
warmup_steps = sum(mcmc.get_extra_fields()["num_steps"])

mcmc.run(
    rng_key_,
    marriage=dset.MarriageScaled.values,
    divorce=dset.DivorceScaled.values,
    extra_fields=("num_steps",),
)
total_steps = sum(mcmc.get_extra_fields()["num_steps"]) + warmup_steps

print(
    f"Number of warmup steps: {warmup_steps}.  Total number of gradient evaluations: {total_steps}"
)

warmup: 100%|██████████| 1000/1000 [00:02<00:00, 407.77it/s, 1 steps of size 6.75e-01. acc. prob=0.79]
sample: 100%|██████████| 2000/2000 [00:03<00:00, 508.24it/s, 7 steps of size 6.75e-01. acc. prob=0.94]

Number of warmup steps: 4529.  Total number of gradient evaluations: 15611

参考文献

McElreath, R. (2016). Statistical Rethinking: A Bayesian Course with Examples in R and Stan CRC Press.
Stan Development Team. Stan 用户指南
Goodman, N.D. 和 StuhlMueller, A. (2014)。概率编程语言的设计与实现
Pyro 开发团队。Poutine：Pyro 中使用效果处理器编程指南
Hoffman, M.D.，Gelman, A. (2011)。The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.
Betancourt, M. (2017). A Conceptual Introduction to Hamiltonian Monte Carlo.
JAX 开发团队 (2018)。Python+NumPy 程序的组合变换：求导、向量化、JIT 到 GPU/TPU 等
Gelman, A.，Hwang, J.，和 Vehtari A. 理解贝叶斯模型的预测信息准则