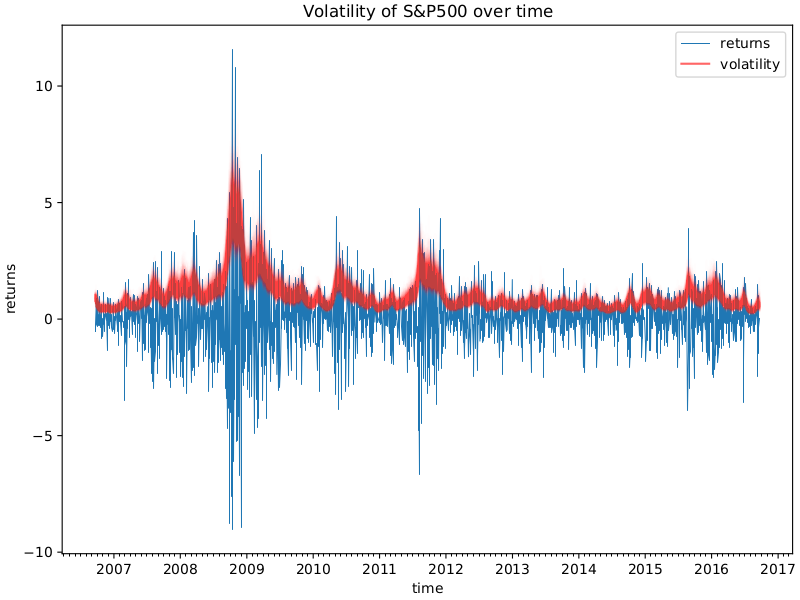
示例：随机波动率

生成模型

\begin{align} \sigma & \sim \text{Exponential}(50) \\ \nu & \sim \text{Exponential}(.1) \\ s_i & \sim \text{Normal}(s_{i-1}, \sigma^{- 2}) \\ r_i & \sim \text{StudentT}(\nu, 0, \exp(s_i)) \end{align}

此示例来自 PyMC3 [1]，它本身改编自 [2] 中的原始实验。在 Pyro 中翻译此示例的讨论出现在 [3] 中。

我们以此示例来说明如何使用函数式接口 hmc。但是，我们建议读者使用 MCMC 类，如其他示例所示，因为它更稳定并支持更多功能。

参考文献

1. 随机波动率模型, https://docs.pymc.io/notebooks/stochastic_volatility.html

2. No-U-Turn 采样器：自适应设置汉密尔顿蒙特卡洛中的路径长度, https://arxiv.org/pdf/1111.4246.pdf

3. Pyro 论坛讨论, https://forum.pyro.ai/t/problems-transforming-a-pymc3-model-to-pyro-mcmc/208/14

import argparse
import os

import matplotlib
import matplotlib.dates as mdates
import matplotlib.pyplot as plt

import jax.numpy as jnp
import jax.random as random

import numpyro
import numpyro.distributions as dist
from numpyro.examples.datasets import SP500, load_dataset
from numpyro.infer.hmc import hmc
from numpyro.infer.util import initialize_model
from numpyro.util import fori_collect

matplotlib.use("Agg")  # noqa: E402


def model(returns):
    step_size = numpyro.sample("sigma", dist.Exponential(50.0))
    s = numpyro.sample(
        "s", dist.GaussianRandomWalk(scale=step_size, num_steps=jnp.shape(returns)[0])
    )
    nu = numpyro.sample("nu", dist.Exponential(0.1))
    return numpyro.sample(
        "r", dist.StudentT(df=nu, loc=0.0, scale=jnp.exp(s)), obs=returns
    )


def print_results(posterior, dates):
    def _print_row(values, row_name=""):
        quantiles = jnp.array([0.2, 0.4, 0.5, 0.6, 0.8])
        row_name_fmt = "{:>8}"
        header_format = row_name_fmt + "{:>12}" * 5
        row_format = row_name_fmt + "{:>12.3f}" * 5
        columns = ["(p{})".format(int(q * 100)) for q in quantiles]
        q_values = jnp.quantile(values, quantiles, axis=0)
        print(header_format.format("", *columns))
        print(row_format.format(row_name, *q_values))
        print("\n")

    print("=" * 20, "sigma", "=" * 20)
    _print_row(posterior["sigma"])
    print("=" * 20, "nu", "=" * 20)
    _print_row(posterior["nu"])
    print("=" * 20, "volatility", "=" * 20)
    for i in range(0, len(dates), 180):
        _print_row(jnp.exp(posterior["s"][:, i]), dates[i])


def main(args):
    _, fetch = load_dataset(SP500, shuffle=False)
    dates, returns = fetch()
    init_rng_key, sample_rng_key = random.split(random.PRNGKey(args.rng_seed))
    model_info = initialize_model(init_rng_key, model, model_args=(returns,))
    init_kernel, sample_kernel = hmc(model_info.potential_fn, algo="NUTS")
    hmc_state = init_kernel(
        model_info.param_info, args.num_warmup, rng_key=sample_rng_key
    )
    hmc_states = fori_collect(
        args.num_warmup,
        args.num_warmup + args.num_samples,
        sample_kernel,
        hmc_state,
        transform=lambda hmc_state: model_info.postprocess_fn(hmc_state.z),
        progbar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
    )
    print_results(hmc_states, dates)

    fig, ax = plt.subplots(figsize=(8, 6), constrained_layout=True)
    dates = mdates.num2date(mdates.datestr2num(dates))
    ax.plot(dates, returns, lw=0.5)
    # format the ticks
    ax.xaxis.set_major_locator(mdates.YearLocator())
    ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y"))
    ax.xaxis.set_minor_locator(mdates.MonthLocator())

    ax.plot(dates, jnp.exp(hmc_states["s"].T), "r", alpha=0.01)
    legend = ax.legend(["returns", "volatility"], loc="upper right")
    legend.legend_handles[1].set_alpha(0.6)
    ax.set(xlabel="time", ylabel="returns", title="Volatility of S&P500 over time")

    plt.savefig("stochastic_volatility_plot.pdf")


if __name__ == "__main__":
    assert numpyro.__version__.startswith("0.18.0")
    parser = argparse.ArgumentParser(description="Stochastic Volatility Model")
    parser.add_argument("-n", "--num-samples", nargs="?", default=600, type=int)
    parser.add_argument("--num-warmup", nargs="?", default=600, type=int)
    parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
    parser.add_argument(
        "--rng_seed", default=21, type=int, help="random number generator seed"
    )
    args = parser.parse_args()

    numpyro.set_platform(args.device)

    main(args)