时间序列预测
在本教程中,我们将演示如何在 NumPyro 中构建时间序列预测模型。具体来说,我们将复制 Rlgt: 具有趋势修改的贝叶斯指数平滑模型 包中的 季节性、全局趋势 (SGT) 模型。本教程将使用的时间序列数据是 lynx 数据集,其中包含 1821 年至 1934 年加拿大每年捕获的猞猁数量。
[ ]:
!pip install -q numpyro@git+https://github.com/pyro-ppl/numpyro
[1]:
import os
from IPython.display import set_matplotlib_formats
import matplotlib.pyplot as plt
import pandas as pd
from jax import random
import jax.numpy as jnp
import numpyro
from numpyro.contrib.control_flow import scan
from numpyro.diagnostics import autocorrelation, hpdi
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, Predictive
if "NUMPYRO_SPHINXBUILD" in os.environ:
set_matplotlib_formats("svg")
numpyro.set_host_device_count(4)
assert numpyro.__version__.startswith("0.18.0")
数据
首先,让我们导入并查看数据集。
[2]:
URL = "https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/datasets/lynx.csv"
lynx = pd.read_csv(URL, index_col=0)
data = lynx["value"].values
print("Length of time series:", data.shape[0])
plt.figure(figsize=(8, 4))
plt.plot(lynx["time"], data)
plt.show()
Length of time series: 114
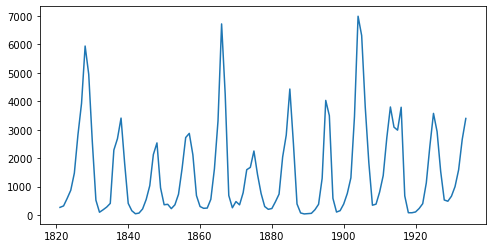
该时间序列的长度为 114(每年一个数据点),通过查看图表,我们可以观察到数据集中的季节性,即特定时间段内相似模式的周期性出现。例如,在该数据集中,我们观察到每 10 年出现一次周期性模式,但每 40 年捕获数量也会出现一个不太明显但清晰的峰值。让我们看看是否能在 NumPyro 中模拟这种效应。
在本教程中,我们将使用前 80 个值进行训练,使用后 34 个值进行测试。
[3]:
y_train, y_test = jnp.array(data[:80], dtype=jnp.float32), data[80:]
模型
我们将使用的模型称为 季节性、全局趋势 模型,该模型在针对 M-3 竞赛 中的 3003 个时间序列进行测试时,已知其性能优于最初参与竞赛的其他模型
\begin{align} \text{预期值}_{t} &= \text{基准值}_{t-1} + \text{趋势系数} \times \text{基准值}_{t-1}^{\text{趋势幂次}} + \text{季节分量}_t \times \text{基准值}_{t-1}^{\text{季节幂次}}, \\ \sigma_{t} &= \sigma \times \text{预期值}_{t}^{\text{幂次 x}} + \text{偏移量}, \\ y_{t} &\sim \text{学生 T 分布}(\nu, \text{预期值}_{t}, \sigma_{t}) \end{align}
,其中 level 和 s 遵循以下递归规则
\begin{align} \text{level-p} &= \begin{cases} y_t - \text{s}_t \times \text{level}_{t-1}^{\text{pow-season}} & \text{if } t \le \text{seasonality}, \\ \text{Average} \left[y(t - \text{seasonality} + 1), \ldots, y(t)\right] & \text{otherwise}, \end{cases} \\ \text{level}_{t} &= \text{level-sm} \times \text{level-p} + (1 - \text{level-sm}) \times \text{level}_{t-1}, \\ \text{s}_{t + \text{seasonality}} &= \text{s-sm} \times \frac{y_{t} - \text{level}_{t}}{\text{level}_{t-1}^{\text{pow-trend}}} + (1 - \text{s-sm}) \times \text{s}_{t}. \end{align}
有关 SGT 模型的更详细解释可在 Rlgt 包作者的此小插曲中找到。此处我们总结该模型的核心思想
学生 t 分布,其尾部比正态分布更厚重,用于似然函数。
期望值
exp_val由一个趋势分量和一个季节性分量组成趋势由映射 \(x \mapsto x + ax^b\) 控制,其中 \(x\) 是
level,\(a\) 是coef_trend,\(b\) 是pow_trend。请注意,当 \(b \sim 0\) 时,趋势是线性的,\(a\) 是斜率;当 \(b \sim 1\) 时,趋势是指数的,\(a\) 是增长率。因此,该函数可以覆盖广泛的趋势类别。当时间变化时,
level和s会更新到新值。系数level_sm和s_sm用于使过渡平滑。
当
powx接近 \(0\) 时,误差 \(\sigma_t\) 将几乎恒定,而当powx接近 \(1\) 时,误差将与期望值成比例。SGT 有多种变体。在本教程中,我们使用广义季节性和季节平均方法。
我们现在准备使用 NumPyro 基本构件指定模型。在 NumPyro 中,我们使用基本构件 sample(name, prior) 声明一个具有相应 prior 的潜在随机变量。这些基本构件可以根据 NumPyro 推断算法在后端使用的效果处理器具有自定义解释。例如,我们可以使用 condition 处理器在特定值上进行条件化,或者使用 trace 处理器在执行跟踪中记录这些采样点的值。请注意,这些细节对于指定模型或运行推断并不重要,但好奇的读者可以阅读 Pyro 中关于效果处理器的教程。
[4]:
def sgt(y, seasonality, future=0):
# heuristically, standard derivation of Cauchy prior depends on
# the max value of data
cauchy_sd = jnp.max(y) / 150
# NB: priors' parameters are taken from
# https://github.com/cbergmeir/Rlgt/blob/master/Rlgt/R/rlgtcontrol.R
nu = numpyro.sample("nu", dist.Uniform(2, 20))
powx = numpyro.sample("powx", dist.Uniform(0, 1))
sigma = numpyro.sample("sigma", dist.HalfCauchy(cauchy_sd))
offset_sigma = numpyro.sample(
"offset_sigma", dist.TruncatedCauchy(low=1e-10, loc=1e-10, scale=cauchy_sd)
)
coef_trend = numpyro.sample("coef_trend", dist.Cauchy(0, cauchy_sd))
pow_trend_beta = numpyro.sample("pow_trend_beta", dist.Beta(1, 1))
# pow_trend takes values from -0.5 to 1
pow_trend = 1.5 * pow_trend_beta - 0.5
pow_season = numpyro.sample("pow_season", dist.Beta(1, 1))
level_sm = numpyro.sample("level_sm", dist.Beta(1, 2))
s_sm = numpyro.sample("s_sm", dist.Uniform(0, 1))
init_s = numpyro.sample("init_s", dist.Cauchy(0, y[:seasonality] * 0.3))
def transition_fn(carry, t):
level, s, moving_sum = carry
season = s[0] * level**pow_season
exp_val = level + coef_trend * level**pow_trend + season
exp_val = jnp.clip(exp_val, 0)
# use expected vale when forecasting
y_t = jnp.where(t >= N, exp_val, y[t])
moving_sum = (
moving_sum + y[t] - jnp.where(t >= seasonality, y[t - seasonality], 0.0)
)
level_p = jnp.where(t >= seasonality, moving_sum / seasonality, y_t - season)
level = level_sm * level_p + (1 - level_sm) * level
level = jnp.clip(level, 0)
new_s = (s_sm * (y_t - level) / season + (1 - s_sm)) * s[0]
# repeat s when forecasting
new_s = jnp.where(t >= N, s[0], new_s)
s = jnp.concatenate([s[1:], new_s[None]], axis=0)
omega = sigma * exp_val**powx + offset_sigma
y_ = numpyro.sample("y", dist.StudentT(nu, exp_val, omega))
return (level, s, moving_sum), y_
N = y.shape[0]
level_init = y[0]
s_init = jnp.concatenate([init_s[1:], init_s[:1]], axis=0)
moving_sum = level_init
with numpyro.handlers.condition(data={"y": y[1:]}):
_, ys = scan(
transition_fn, (level_init, s_init, moving_sum), jnp.arange(1, N + future)
)
if future > 0:
numpyro.deterministic("y_forecast", ys[-future:])
请注意,level 和 s 会递归更新,同时我们在每个时间步收集期望值。NumPyro 在后端使用 JAX 对 NUTS 算法的许多关键部分进行 JIT 编译,包括 Verlet 积分器和树构建过程。然而,如果在模型中使用 Python 的 for 循环这样做会导致模型的编译时间很长,因此我们使用 scan——它是 lax.scan 的一个封装,支持 NumPyro 基本构件和处理器。有关使用此实用程序的详细解释可在NumPyro 文档中找到。此处我们使用它收集 y 值,而三元组 (level, s, moving_sum) 扮演着携带状态的角色。
另一点需要注意的是,我们没有在 transition_fn 中声明观测站点 y
numpyro.sample("y", dist.StudentT(nu, exp_val, omega), obs=y[t])
,而是使用了 condition 处理器。原因是我们也想将此模型用于预测。在预测中,y 的未来值是不可观测的,因此当 t >= len(y) 时,obs=y[t] 没有意义(注意:JAX 不会引发索引越界错误,例如 jnp.arange(3)[10] == 2)。使用 condition,当 scan 的长度大于条件化/观测站点的长度时,未观测的值将从该站点的分布中进行采样。
推断
首先,我们想为 seasonality 选择一个好的值。按照 Rlgt 中的演示,我们将设置 seasonality=38。事实上,通过查看训练数据的图表可以猜到这个值,其中二阶季节性效应的周期性约为 \(40\) 年。注意,\(38\) 也是自相关最高的滞后之一。
[5]:
print("Lag values sorted according to their autocorrelation values:\n")
print(jnp.argsort(autocorrelation(y_train))[::-1])
Lag values sorted according to their autocorrelation values:
[ 0 67 57 38 68 1 29 58 37 56 28 10 19 39 66 78 47 77 9 79 48 76 30 18
20 11 46 59 69 27 55 36 2 8 40 49 17 21 75 12 65 45 31 26 7 54 35 41
50 3 22 60 70 16 44 13 6 25 74 53 42 32 23 43 51 4 15 14 34 24 5 52
73 64 33 71 72 61 63 62]
现在,让我们运行 \(4\) 条 MCMC 链(使用 No-U-Turn Sampler 算法),每条链进行 \(5000\) 次预热步和 \(5000\) 次采样步。返回的值将是 \(20000\) 个样本的集合。
[6]:
%%time
kernel = NUTS(sgt)
mcmc = MCMC(kernel, num_warmup=5000, num_samples=5000, num_chains=4)
mcmc.run(random.PRNGKey(0), y_train, seasonality=38)
mcmc.print_summary()
samples = mcmc.get_samples()
mean std median 5.0% 95.0% n_eff r_hat
coef_trend 32.33 123.99 12.07 -91.43 157.37 1307.74 1.00
init_s[0] 84.35 105.16 61.08 -59.71 232.37 4053.35 1.00
init_s[1] -21.48 72.05 -26.11 -130.13 94.34 1038.51 1.01
init_s[2] 26.08 92.13 13.57 -114.83 156.16 1559.02 1.00
init_s[3] 122.52 123.56 102.67 -59.39 305.43 4317.17 1.00
init_s[4] 443.91 254.12 395.89 69.08 789.27 3090.34 1.00
init_s[5] 1163.56 491.37 1079.23 481.92 1861.90 1562.40 1.00
init_s[6] 1968.70 649.68 1860.04 902.00 2910.49 1974.42 1.00
init_s[7] 3652.34 1107.27 3505.37 1967.67 5383.26 1669.91 1.00
init_s[8] 2593.04 831.42 2452.27 1317.67 3858.55 1805.87 1.00
init_s[9] 947.28 422.29 885.72 311.39 1589.56 3355.27 1.00
init_s[10] 44.09 102.92 28.38 -105.25 203.73 1367.99 1.00
init_s[11] -2.25 52.92 -2.71 -86.51 72.90 611.35 1.01
init_s[12] -12.22 64.98 -13.67 -110.07 85.65 892.13 1.01
init_s[13] 74.43 106.48 53.13 -79.73 225.92 658.08 1.01
init_s[14] 332.98 255.28 281.72 -11.18 697.96 3685.55 1.00
init_s[15] 965.80 389.00 893.29 373.98 1521.59 2575.80 1.00
init_s[16] 1261.12 469.99 1191.83 557.98 1937.38 2300.48 1.00
init_s[17] 1372.34 559.14 1274.21 483.96 2151.94 2007.79 1.00
init_s[18] 611.20 313.13 546.56 167.97 1087.74 2854.06 1.00
init_s[19] 17.81 87.79 8.93 -118.64 143.96 5689.95 1.00
init_s[20] -31.84 66.70 -25.15 -146.89 58.97 3083.09 1.00
init_s[21] -14.01 44.74 -5.80 -86.03 42.99 2118.09 1.00
init_s[22] -2.26 42.99 -2.39 -61.40 66.34 3022.51 1.00
init_s[23] 43.53 90.60 29.14 -82.56 167.89 3230.17 1.00
init_s[24] 509.69 326.73 453.22 44.04 975.15 2087.02 1.00
init_s[25] 919.23 431.15 837.03 284.54 1563.05 3257.27 1.00
init_s[26] 1783.39 697.15 1660.09 720.83 2811.83 1730.70 1.00
init_s[27] 1247.60 461.26 1172.88 544.44 1922.68 1573.09 1.00
init_s[28] 217.92 169.08 191.38 -29.78 456.65 4899.06 1.00
init_s[29] -7.43 82.23 -12.99 -133.20 118.31 7588.25 1.00
init_s[30] -6.69 86.99 -17.03 -130.99 125.43 1687.37 1.00
init_s[31] -35.24 71.31 -35.75 -148.09 76.96 5462.22 1.00
init_s[32] -8.63 80.39 -14.95 -138.34 113.89 6626.25 1.00
init_s[33] 117.38 148.71 91.69 -78.12 316.69 2424.57 1.00
init_s[34] 502.79 297.08 448.55 87.88 909.45 1863.99 1.00
init_s[35] 1064.57 445.88 984.10 391.61 1710.35 2584.45 1.00
init_s[36] 1849.48 632.44 1763.31 861.63 2800.25 1866.47 1.00
init_s[37] 1452.62 546.57 1382.62 635.28 2257.04 2343.09 1.00
level_sm 0.00 0.00 0.00 0.00 0.00 7829.05 1.00
nu 12.17 4.73 12.31 5.49 19.99 4979.84 1.00
offset_sigma 31.82 31.84 22.43 0.01 73.13 1442.32 1.00
pow_season 0.09 0.04 0.09 0.01 0.15 1091.99 1.00
pow_trend_beta 0.26 0.18 0.24 0.00 0.52 199.20 1.01
powx 0.62 0.13 0.62 0.40 0.84 2476.16 1.00
s_sm 0.08 0.09 0.05 0.00 0.18 5866.57 1.00
sigma 9.67 9.87 6.61 0.35 20.60 2376.07 1.00
Number of divergences: 4568
CPU times: user 1min 17s, sys: 108 ms, total: 1min 18s
Wall time: 41.2 s
预测
给定从 mcmc 中得到的 samples,我们想对测试数据集 y_test 进行预测。NumPyro 提供了一个便捷的实用工具 Predictive 来获取预测分布。让我们看看如何使用它来获取预测值。
请注意,在上面定义的 sgt 模型中,有一个关键字 future 控制模型的执行 - 取决于 future > 0 还是 future == 0。以下代码预测原始时间序列的最后 34 个值。
[7]:
predictive = Predictive(sgt, samples, return_sites=["y_forecast"])
forecast_marginal = predictive(random.PRNGKey(1), y_train, seasonality=38, future=34)[
"y_forecast"
]
让我们计算 sMAPE、预测的均方根误差,并用平均预测和 90% 最高后验密度区间 (HPDI) 可视化结果。
[8]:
y_pred = jnp.mean(forecast_marginal, axis=0)
sMAPE = jnp.mean(jnp.abs(y_pred - y_test) / (y_pred + y_test)) * 200
msqrt = jnp.sqrt(jnp.mean((y_pred - y_test) ** 2))
print("sMAPE: {:.2f}, rmse: {:.2f}".format(sMAPE, msqrt))
sMAPE: 63.93, rmse: 1249.29
最后,让我们绘制结果图来验证我们是否得到了期望的结果。
[9]:
plt.figure(figsize=(8, 4))
plt.plot(lynx["time"], data)
t_future = lynx["time"][80:]
hpd_low, hpd_high = hpdi(forecast_marginal)
plt.plot(t_future, y_pred, lw=2)
plt.fill_between(t_future, hpd_low, hpd_high, alpha=0.3)
plt.title("Forecasting lynx dataset with SGT model (90% HPDI)")
plt.show()
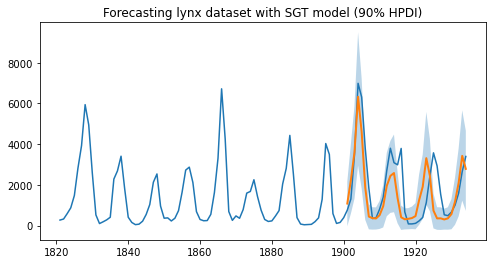
正如我们所观察到的,该模型能够学习一阶和二阶季节性效应,即周期性约为 10 的循环模式,以及大约每 40 年出现一次的峰值。此外,我们不仅有预测的点估计,还可以利用模型中的不确定性估计来限制我们的预测。
致谢
我们要感谢 Slawek Smyl 提供的许多有用的资源和建议。如果没有 JAX 和 XLA 团队的支持,快速推断是不可能实现的,因此我们要感谢他们为我们提供如此优秀的开源平台,以及他们对我们功能请求和 bug 报告的快速响应。
参考文献
[1] Rlgt: Bayesian Exponential Smoothing Models with Trend Modifications, Slawek Smyl, Christoph Bergmeir, Erwin Wibowo, To Wang Ng, Trustees of Columbia University