示例：Neal's Funnel

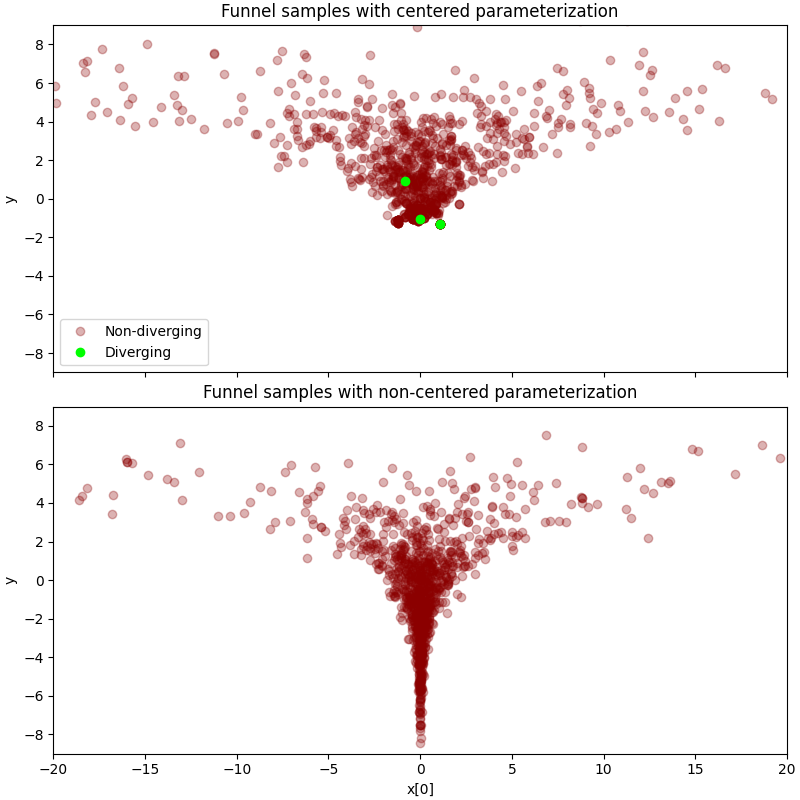
本示例改编自 [1]，说明了如何利用非中心化参数化，使用 reparam 处理器。我们将检验两种参数化类型在 10 维 Neal's Funnel 分布上的差异。正如我们将看到的，如果使用中心化参数化，HMC 在 Funnel 的颈部会遇到困难。相反，使用非中心化参数化可以解决这个问题。

在 NumPyro 中，通过 LocScaleReparam 或 TransformReparam 使用非中心化参数化，与 [2] 中介绍的自动重参数化技术效果相同。

参考文献

1. Stan 用户指南, https://mc-stan.org/docs/2_19/stan-users-guide/reparameterization-section.html

2. Maria I. Gorinova, Dave Moore, Matthew D. Hoffman (2019), “概率程序的自动重参数化”, (https://arxiv.org/abs/1906.03028)

import argparse
import os

import matplotlib.pyplot as plt

from jax import random
import jax.numpy as jnp

import numpyro
import numpyro.distributions as dist
from numpyro.handlers import reparam
from numpyro.infer import MCMC, NUTS, Predictive
from numpyro.infer.reparam import LocScaleReparam


def model(dim=10):
    y = numpyro.sample("y", dist.Normal(0, 3))
    numpyro.sample("x", dist.Normal(jnp.zeros(dim - 1), jnp.exp(y / 2)))


reparam_model = reparam(model, config={"x": LocScaleReparam(0)})


def run_inference(model, args, rng_key):
    kernel = NUTS(model)
    mcmc = MCMC(
        kernel,
        num_warmup=args.num_warmup,
        num_samples=args.num_samples,
        num_chains=args.num_chains,
        progress_bar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
    )
    mcmc.run(rng_key)
    mcmc.print_summary(exclude_deterministic=False)
    return mcmc


def main(args):
    rng_key = random.PRNGKey(0)

    # do inference with centered parameterization
    print(
        "============================= Centered Parameterization =============================="
    )
    mcmc = run_inference(model, args, rng_key)
    samples = mcmc.get_samples()
    diverging = mcmc.get_extra_fields()["diverging"]

    # do inference with non-centered parameterization
    print(
        "\n=========================== Non-centered Parameterization ============================"
    )
    reparam_mcmc = run_inference(reparam_model, args, rng_key)
    reparam_samples = reparam_mcmc.get_samples()
    reparam_diverging = reparam_mcmc.get_extra_fields()["diverging"]
    # collect deterministic sites
    reparam_samples = Predictive(
        reparam_model, reparam_samples, return_sites=["x", "y"]
    )(random.PRNGKey(1))

    # make plots
    fig, (ax1, ax2) = plt.subplots(
        2, 1, sharex=True, figsize=(8, 8), constrained_layout=True
    )

    ax1.plot(
        samples["x"][~diverging, 0],
        samples["y"][~diverging],
        "o",
        color="darkred",
        alpha=0.3,
        label="Non-diverging",
    )
    ax1.plot(
        samples["x"][diverging, 0],
        samples["y"][diverging],
        "o",
        color="lime",
        label="Diverging",
    )
    ax1.set(
        xlim=(-20, 20),
        ylim=(-9, 9),
        ylabel="y",
        title="Funnel samples with centered parameterization",
    )
    ax1.legend()

    ax2.plot(
        reparam_samples["x"][~reparam_diverging, 0],
        reparam_samples["y"][~reparam_diverging],
        "o",
        color="darkred",
        alpha=0.3,
    )
    ax2.plot(
        reparam_samples["x"][reparam_diverging, 0],
        reparam_samples["y"][reparam_diverging],
        "o",
        color="lime",
    )
    ax2.set(
        xlim=(-20, 20),
        ylim=(-9, 9),
        xlabel="x[0]",
        ylabel="y",
        title="Funnel samples with non-centered parameterization",
    )

    plt.savefig("funnel_plot.pdf")


if __name__ == "__main__":
    assert numpyro.__version__.startswith("0.18.0")
    parser = argparse.ArgumentParser(
        description="Non-centered reparameterization example"
    )
    parser.add_argument("-n", "--num-samples", nargs="?", default=1000, type=int)
    parser.add_argument("--num-warmup", nargs="?", default=1000, type=int)
    parser.add_argument("--num-chains", nargs="?", default=1, type=int)
    parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
    args = parser.parse_args()

    numpyro.set_platform(args.device)
    numpyro.set_host_device_count(args.num_chains)

    main(args)