注意
跳到末尾以下载完整的示例代码。
示例:正弦偏斜正弦(二元 von Mises)混合
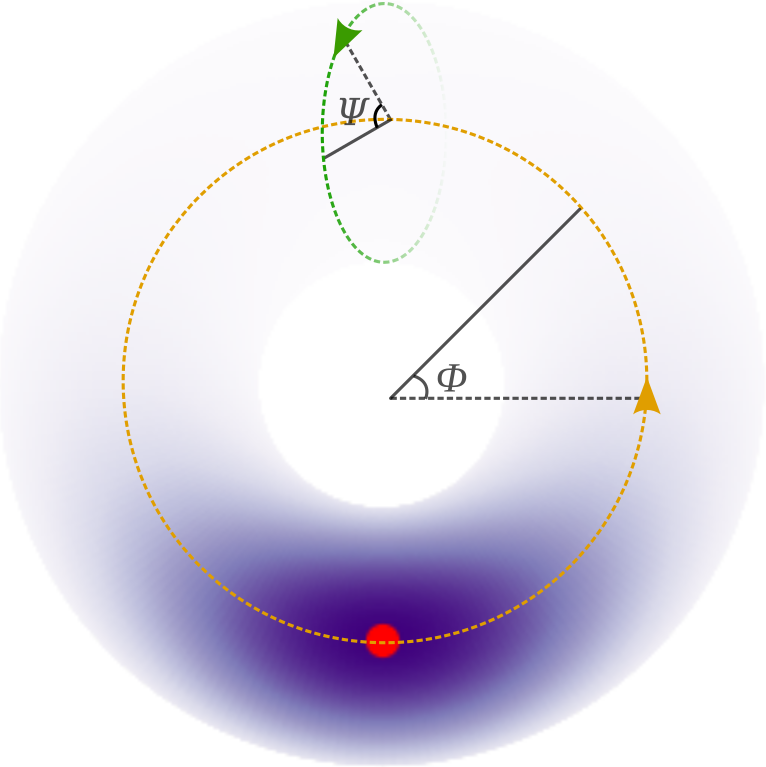
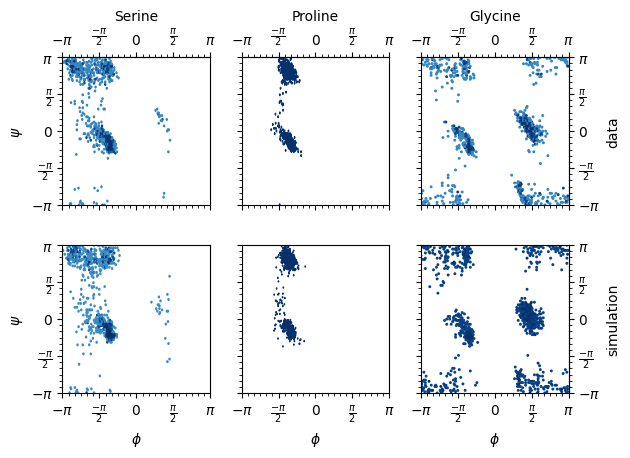
这个例子将蛋白质骨架中出现的二面角建模为偏斜方向分布的混合。这些骨架角对称为 \(\phi\) 和 \(\psi\),是蛋白质折叠的典型表示。在此模型中,我们将第三个二面角 (omega) 固定,因为它通常只取 0 和 pi 弧度,其中后者是最常见的。我们使用正弦分布 [1] 将角对建模为环面上的分布,并使用正弦偏斜 [2] 打破点对称(环面对称)。
参考文献
Singh 等人 (2002). 两个相关圆形变量的概率模型。Biometrika。
Jose Ameijeiras-Alonso 和 Christophe Ley (2021). 正弦偏斜环面分布及其在蛋白质生物信息学中的应用。Biostatistics。
import argparse
import math
from math import pi
import matplotlib.colors
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from jax import numpy as jnp, random
import numpyro
from numpyro.distributions import (
Beta,
Categorical,
Dirichlet,
Gamma,
Normal,
SineBivariateVonMises,
SineSkewed,
Uniform,
VonMises,
)
from numpyro.distributions.transforms import L1BallTransform
from numpyro.examples.datasets import NINE_MERS, load_dataset
from numpyro.infer import MCMC, NUTS, Predictive, init_to_value
from numpyro.infer.reparam import CircularReparam
AMINO_ACIDS = [
"M",
"N",
"I",
"F",
"E",
"L",
"R",
"D",
"G",
"K",
"Y",
"T",
"H",
"S",
"P",
"A",
"V",
"Q",
"W",
"C",
]
# The support of the von Mises is [-π,π) with a periodic boundary at ±π. However, the support of
# the implemented von Mises distribution is just the interval [-π,π) without the periodic boundary. If the
# loc is close to one of the boundaries (-π or π), the sampler must traverse the entire interval to cross the
# boundary. This produces a bias, especially if the concentration is high. The interval around
# zero will have a low probability, making the jump to the other boundary unlikely for the sampler.
# Using the `CircularReparam` introduces the periodic boundary by transforming the real line to [-π,π).
# The sampler can sample from the real line, thus crossing the periodic boundary without having to traverse the
# the entire interval, which eliminates the bias.
@numpyro.handlers.reparam(
config={"phi_loc": CircularReparam(), "psi_loc": CircularReparam()}
)
def ss_model(data, num_data, num_mix_comp=2):
# Mixture prior
mix_weights = numpyro.sample("mix_weights", Dirichlet(jnp.ones((num_mix_comp,))))
# Hprior BvM
# Bayesian Inference and Decision Theory by Kathryn Blackmond Laskey
beta_mean_phi = numpyro.sample("beta_mean_phi", Uniform(0.0, 1.0))
beta_count_phi = numpyro.sample(
"beta_count_phi", Gamma(1.0, 1.0 / num_mix_comp)
) # shape, rate
halpha_phi = beta_mean_phi * beta_count_phi
beta_mean_psi = numpyro.sample("beta_mean_psi", Uniform(0, 1.0))
beta_count_psi = numpyro.sample(
"beta_count_psi", Gamma(1.0, 1.0 / num_mix_comp)
) # shape, rate
halpha_psi = beta_mean_psi * beta_count_psi
with numpyro.plate("mixture", num_mix_comp):
# BvM priors
# Place gap in forbidden region of the Ramachandran plot (protein backbone dihedral angle pairs)
phi_loc = numpyro.sample("phi_loc", VonMises(pi, 2.0))
psi_loc = numpyro.sample("psi_loc", VonMises(0.0, 0.1))
phi_conc = numpyro.sample(
"phi_conc", Beta(halpha_phi, beta_count_phi - halpha_phi)
)
psi_conc = numpyro.sample(
"psi_conc", Beta(halpha_psi, beta_count_psi - halpha_psi)
)
corr_scale = numpyro.sample("corr_scale", Beta(2.0, 10.0))
# Skewness prior
ball_transform = L1BallTransform()
skewness = numpyro.sample("skewness", Normal(0, 0.5).expand((2,)).to_event(1))
skewness = ball_transform(skewness)
with numpyro.plate("obs_plate", num_data, dim=-1):
assign = numpyro.sample(
"mix_comp", Categorical(mix_weights), infer={"enumerate": "parallel"}
)
sine = SineBivariateVonMises(
phi_loc=phi_loc[assign],
psi_loc=psi_loc[assign],
phi_concentration=1000 * phi_conc[assign],
psi_concentration=1000 * psi_conc[assign],
weighted_correlation=corr_scale[assign],
)
return numpyro.sample("phi_psi", SineSkewed(sine, skewness[assign]), obs=data)
def run_hmc(rng_key, model, data, num_mix_comp, args, bvm_init_locs):
kernel = NUTS(model, init_strategy=init_to_value(values=bvm_init_locs))
mcmc = MCMC(kernel, num_samples=args.num_samples, num_warmup=args.num_warmup)
mcmc.run(rng_key, data, len(data), num_mix_comp)
mcmc.print_summary()
post_samples = mcmc.get_samples()
return post_samples
def fetch_aa_dihedrals(aa):
_, fetch = load_dataset(NINE_MERS, split=aa)
return jnp.stack(fetch())
def num_mix_comps(amino_acid):
num_mix = {"G": 10, "P": 7}
return num_mix.get(amino_acid, 9)
def ramachandran_plot(data, pred_data, aas, file_name="ssbvm_mixture.png"):
amino_acids = {"S": "Serine", "P": "Proline", "G": "Glycine"}
fig, axss = plt.subplots(2, len(aas))
cdata = data
for i in range(len(axss)):
if i == 1:
cdata = pred_data
for ax, aa in zip(axss[i], aas):
aa_data = cdata[aa]
nbins = 50
ax.hexbin(
aa_data[..., 0].reshape(-1),
aa_data[..., 1].reshape(-1),
norm=matplotlib.colors.LogNorm(),
bins=nbins,
gridsize=100,
cmap="Blues",
)
# label the contours
ax.set_aspect("equal", "box")
ax.set_xlim([-math.pi, math.pi])
ax.set_ylim([-math.pi, math.pi])
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 12))
ax.xaxis.set_major_formatter(plt.FuncFormatter(multiple_formatter()))
ax.yaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.yaxis.set_minor_locator(plt.MultipleLocator(np.pi / 12))
ax.yaxis.set_major_formatter(plt.FuncFormatter(multiple_formatter()))
if i == 0:
axtop = ax.secondary_xaxis("top")
axtop.set_xlabel(amino_acids[aa])
axtop.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
axtop.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 12))
axtop.xaxis.set_major_formatter(plt.FuncFormatter(multiple_formatter()))
if i == 1:
ax.set_xlabel(r"$\phi$")
for i in range(len(axss)):
axss[i, 0].set_ylabel(r"$\psi$")
axss[i, 0].yaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
axss[i, 0].yaxis.set_minor_locator(plt.MultipleLocator(np.pi / 12))
axss[i, 0].yaxis.set_major_formatter(plt.FuncFormatter(multiple_formatter()))
axright = axss[i, -1].secondary_yaxis("right")
axright.set_ylabel("data" if i == 0 else "simulation")
axright.yaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
axright.yaxis.set_minor_locator(plt.MultipleLocator(np.pi / 12))
axright.yaxis.set_major_formatter(plt.FuncFormatter(multiple_formatter()))
for ax in axss[:, 1:].reshape(-1):
ax.tick_params(labelleft=False)
ax.tick_params(labelleft=False)
for ax in axss[0, :].reshape(-1):
ax.tick_params(labelbottom=False)
ax.tick_params(labelbottom=False)
if file_name:
fig.tight_layout()
plt.savefig(file_name, bbox_inches="tight")
def multiple_formatter(denominator=2, number=np.pi, latex=r"\pi"):
def gcd(a, b):
while b:
a, b = b, a % b
return a
def _multiple_formatter(x, pos):
den = denominator
num = int(np.rint(den * x / number))
com = gcd(num, den)
(num, den) = (int(num / com), int(den / com))
if den == 1:
if num == 0:
return r"$0$"
if num == 1:
return r"$%s$" % latex
elif num == -1:
return r"$-%s$" % latex
else:
return r"$%s%s$" % (num, latex)
else:
if num == 1:
return r"$\frac{%s}{%s}$" % (latex, den)
elif num == -1:
return r"$\frac{-%s}{%s}$" % (latex, den)
else:
return r"$\frac{%s%s}{%s}$" % (num, latex, den)
return _multiple_formatter
def main(args):
data = {}
pred_datas = {}
rng_key = random.PRNGKey(args.rng_seed)
for aa in args.amino_acids:
rng_key, inf_key, pred_key = random.split(rng_key, 3)
data[aa] = fetch_aa_dihedrals(aa)
num_mix_comp = num_mix_comps(aa)
# Use kmeans to initialize the chain location.
kmeans = KMeans(num_mix_comp)
kmeans.fit(data[aa])
means = {
"phi_loc": kmeans.cluster_centers_[:, 0],
"psi_loc": kmeans.cluster_centers_[:, 1],
}
posterior_samples = {
"ss": run_hmc(inf_key, ss_model, data[aa], num_mix_comp, args, means)
}
predictive = Predictive(ss_model, posterior_samples["ss"], parallel=True)
pred_datas[aa] = predictive(pred_key, None, 1, num_mix_comp)["phi_psi"].reshape(
-1, 2
)
ramachandran_plot(data, pred_datas, args.amino_acids)
if __name__ == "__main__":
assert numpyro.__version__.startswith("0.18.0")
parser = argparse.ArgumentParser(
description="Sine-skewed sine (bivariate von mises) mixture model example"
)
parser.add_argument("-n", "--num-samples", nargs="?", default=1000, type=int)
parser.add_argument("--num-warmup", nargs="?", default=500, type=int)
parser.add_argument("--amino-acids", nargs="+", default=["S", "P", "G"])
parser.add_argument("--rng_seed", type=int, default=123)
parser.add_argument("--device", default="gpu", type=str, help='use "cpu" or "gpu".')
args = parser.parse_args()
assert all(aa in AMINO_ACIDS for aa in args.amino_acids), (
f"{list(filter(lambda aa: aa not in AMINO_ACIDS, args.amino_acids))} are not amino acids."
)
main(args)