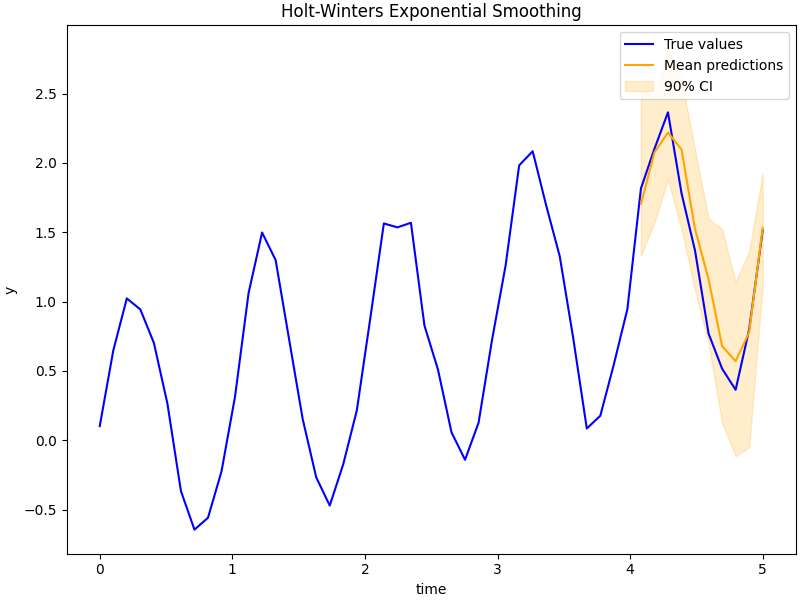
示例：Holt-Winters指数平滑

在此示例中，我们展示了如何实现指数平滑。这旨在作为时间序列预测笔记本的一个简单对应部分。

其思想是我们有一些时间序列

\[y_1, ..., y_T, y_{T+1}, ..., y_{T+H}\]

其中我们在\(y_1, ..., y_T\)上进行训练，并预测\(y_{T+1}, ..., y_{T+H}\)，这里的\(T\)是最大训练时间戳，\(H\)是我们希望预测的未来最大时间步数。

我们将使用优秀书籍《预测：原理与实践》中的更新方程

\[ \begin{align}\begin{aligned}\hat{y}_{t+h|t} = l_t + hb_t + s_{t+h-m(k+1)}\\l_t = \alpha(y_t - s_{t-m}) + (1-\alpha)(l_{t-1} + b_{t-1})\\b_t = \beta^*(l_t-l_{t-1}) + (1-\beta^*)b_{t-1}\\s_t = \gamma(y_t-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-m}\end{aligned}\end{align} \]

其中

• \(\hat{y}_t\)是时间\(t\)的预测值；

• \(h\)是我们希望预测的未来时间步数；

• \(l_t\)是水平项，\(b_t\)是趋势项，\(s_t\)是季节项，

• \(\alpha\)是水平平滑参数，\(\beta^*\)是趋势平滑参数，\(\gamma\)是季节平滑参数。

• \(k\)是\((h-1)/m\)的整数部分（这看起来比实际复杂，它只是取该时间点最新的季节性估计）。

import argparse
import os
import time

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

import jax
from jax import random
import jax.numpy as jnp

import numpyro
from numpyro.contrib.control_flow import scan
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, Predictive

matplotlib.use("Agg")

N_POINTS_PER_UNIT = 10  # number of points to plot for each unit interval


def holt_winters(y, n_seasons, future=0):
    T = y.shape[0]
    level_smoothing = numpyro.sample("level_smoothing", dist.Beta(1, 1))
    trend_smoothing = numpyro.sample("trend_smoothing", dist.Beta(1, 1))
    seasonality_smoothing = numpyro.sample("seasonality_smoothing", dist.Beta(1, 1))
    adj_seasonality_smoothing = seasonality_smoothing * (1 - level_smoothing)
    noise = numpyro.sample("noise", dist.HalfNormal(1))
    level_init = numpyro.sample("level_init", dist.Normal(0, 1))
    trend_init = numpyro.sample("trend_init", dist.Normal(0, 1))
    with numpyro.plate("n_seasons", n_seasons):
        seasonality_init = numpyro.sample("seasonality_init", dist.Normal(0, 1))

    def transition_fn(carry, t):
        previous_level, previous_trend, previous_seasonality = carry
        level = jnp.where(
            t < T,
            level_smoothing * (y[t] - previous_seasonality[0])
            + (1 - level_smoothing) * (previous_level + previous_trend),
            previous_level,
        )
        trend = jnp.where(
            t < T,
            trend_smoothing * (level - previous_level)
            + (1 - trend_smoothing) * previous_trend,
            previous_trend,
        )
        new_season = jnp.where(
            t < T,
            adj_seasonality_smoothing * (y[t] - (previous_level + previous_trend))
            + (1 - adj_seasonality_smoothing) * previous_seasonality[0],
            previous_seasonality[0],
        )
        step = jnp.where(t < T, 1, t - T + 1)
        mu = previous_level + step * previous_trend + previous_seasonality[0]
        pred = numpyro.sample("pred", dist.Normal(mu, noise))

        seasonality = jnp.concatenate(
            [previous_seasonality[1:], new_season[None]], axis=0
        )
        return (level, trend, seasonality), pred

    with numpyro.handlers.condition(data={"pred": y}):
        _, preds = scan(
            transition_fn,
            (level_init, trend_init, seasonality_init),
            jnp.arange(T + future),
        )

    if future > 0:
        numpyro.deterministic("y_forecast", preds[-future:])


def run_inference(model, args, rng_key, y, n_seasons):
    start = time.time()
    sampler = NUTS(model)
    mcmc = MCMC(
        sampler,
        num_warmup=args.num_warmup,
        num_samples=args.num_samples,
        num_chains=args.num_chains,
        progress_bar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
    )
    mcmc.run(rng_key, y=y, n_seasons=n_seasons)
    mcmc.print_summary()
    print("\nMCMC elapsed time:", time.time() - start)
    return mcmc.get_samples()


def predict(model, args, samples, rng_key, y, n_seasons):
    predictive = Predictive(model, samples, return_sites=["y_forecast"])
    return predictive(
        rng_key, y=y, n_seasons=n_seasons, future=args.future * N_POINTS_PER_UNIT
    )["y_forecast"]


def main(args):
    # generate artificial dataset
    rng_key, _ = random.split(random.PRNGKey(0))
    T = args.T
    t = jnp.linspace(0, T + args.future, (T + args.future) * N_POINTS_PER_UNIT)
    y = jnp.sin(2 * np.pi * t) + 0.3 * t + jax.random.normal(rng_key, t.shape) * 0.1
    n_seasons = N_POINTS_PER_UNIT
    y_train = y[: -args.future * N_POINTS_PER_UNIT]
    t_test = t[-args.future * N_POINTS_PER_UNIT :]

    # do inference
    rng_key, _ = random.split(random.PRNGKey(1))
    samples = run_inference(holt_winters, args, rng_key, y_train, n_seasons)

    # do prediction
    rng_key, _ = random.split(random.PRNGKey(2))
    preds = predict(holt_winters, args, samples, rng_key, y_train, n_seasons)
    mean_preds = preds.mean(axis=0)
    hpdi_preds = hpdi(preds)

    # make plots
    fig, ax = plt.subplots(figsize=(8, 6), constrained_layout=True)

    # plot true data and predictions
    ax.plot(t, y, color="blue", label="True values")
    ax.plot(t_test, mean_preds, color="orange", label="Mean predictions")
    ax.fill_between(t_test, *hpdi_preds, color="orange", alpha=0.2, label="90% CI")
    ax.set(xlabel="time", ylabel="y", title="Holt-Winters Exponential Smoothing")
    ax.legend()

    plt.savefig("holt_winters_plot.pdf")


if __name__ == "__main__":
    assert numpyro.__version__.startswith("0.18.0")
    parser = argparse.ArgumentParser(description="Holt-Winters")
    parser.add_argument("--T", nargs="?", default=6, type=int)
    parser.add_argument("--future", nargs="?", default=1, type=int)
    parser.add_argument("-n", "--num-samples", nargs="?", default=1000, type=int)
    parser.add_argument("--num-warmup", nargs="?", default=1000, type=int)
    parser.add_argument("--num-chains", nargs="?", default=1, type=int)
    parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
    args = parser.parse_args()

    numpyro.set_platform(args.device)
    numpyro.set_host_device_count(args.num_chains)

    main(args)