贝叶斯审查数据建模
在此示例中,我们将展示如何使用 NumPyro 对审查数据进行建模。审查是一种测量或观测值仅部分已知的情况。我们将探讨两个示例:一个连续似然和一个离散似然。这两种情况结构相同,但在一个我们想强调的细节上有所不同。建模策略的关键在于 Uber 博客文章“使用 Pyro(一个开源概率编程语言)对审查时间至事件数据进行建模”中描述的累积分布函数 (CDF) 参数化(请参见此处的原始 gist 代码)。
此示例基于 Notebook Bayesian Censoring Data Modeling。
准备 Notebook
[ ]:
!pip install -q numpyro@git+https://github.com/pyro-ppl/numpyro arviz matplotlib preliz pydantic
[ ]:
import os
import arviz as az
from IPython.display import set_matplotlib_formats
from jaxlib.xla_extension import ArrayImpl
import matplotlib.pyplot as plt
import preliz as pz
from pydantic import BaseModel, Field
from jax import random
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.handlers import mask
from numpyro.infer import MCMC, NUTS, Predictive
plt.style.use("bmh")
if "NUMPYRO_SPHINXBUILD" in os.environ:
set_matplotlib_formats("svg")
plt.rcParams["figure.figsize"] = [8, 6]
numpyro.set_host_device_count(n=4)
rng_key = random.PRNGKey(seed=0)
assert numpyro.__version__.startswith("0.18.0")
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"
第一部分:连续分布
我们首先考虑连续情况。我们假设有一个观测值数据集 \(y\),它们在已知阈值处被从下方和上方审查。我们希望估计生成这些观测值的分布参数。我们假设该分布是 Gamma 分布(参数为 \(\alpha\) 和 \(\beta\)),但同样的方法也可用于其他分布。
生成审查数据
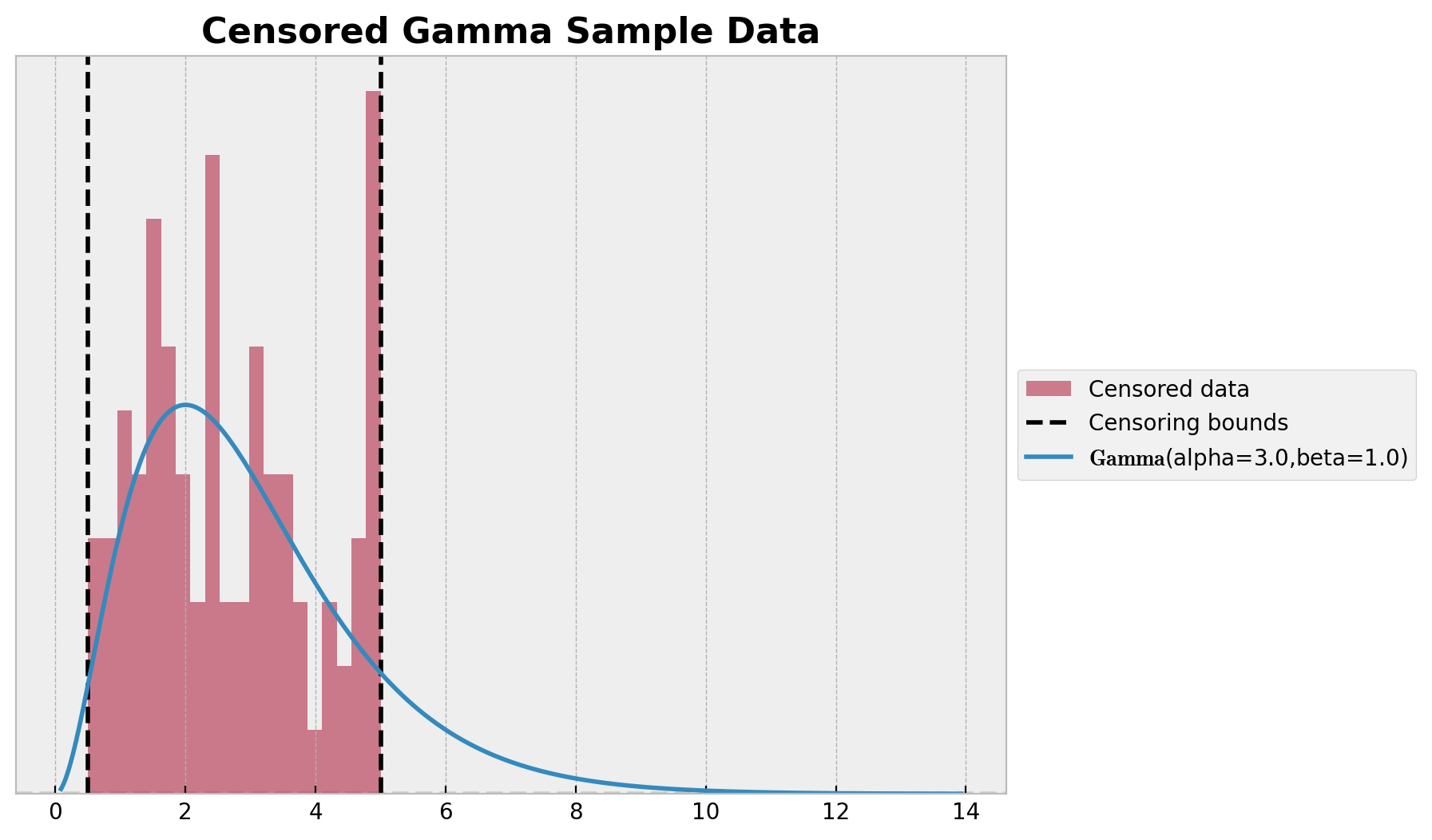
我们从 Gamma 分布生成数据,并将其裁剪至阈值 lower 和 upper 之间。然后绘制数据的直方图和真实的 Gamma 分布。
[2]:
class CensoredGammaDataParams(BaseModel):
alpha: float = Field(..., description="Concentration parameter", gt=0)
beta: float = Field(..., description="Rate parameter", gt=0)
lower: float = Field(..., description="Lower censoring bound", gt=0)
upper: float = Field(..., description="Upper censoring bound", gt=0)
n: int = Field(..., description="Number of samples", gt=0)
def generate_censored_gamma_samples(
rng_key: ArrayImpl, params: CensoredGammaDataParams
) -> ArrayImpl:
raw_samples = dist.Gamma(concentration=params.alpha, rate=params.beta).sample(
rng_key, (params.n,)
)
return jnp.clip(raw_samples, params.lower, params.upper)
censored_gamma_data_params = CensoredGammaDataParams(
alpha=3.0, beta=1.0, lower=0.5, upper=5.0, n=100
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_samples = generate_censored_gamma_samples(
rng_key=rng_subkey, params=censored_gamma_data_params
)
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
ax.set_title("Censored Gamma Sample Data", fontsize=16, fontweight="bold");
朴素模型
在实现审查模型之前,我们先从一个不考虑审查成分的朴素模型开始。我们只使用具有参数 \(\alpha\) 和 \(\beta\) 的 Gamma 分布对数据进行建模。然后绘制参数的后验分布,并与真实值进行比较。
[3]:
def gamma_model(y: ArrayImpl) -> None:
alpha = numpyro.sample("alpha", dist.Exponential(1.0))
beta = numpyro.sample("beta", dist.Exponential(1.0))
numpyro.sample("obs", dist.Gamma(concentration=alpha, rate=beta), obs=y)
class InferenceParams(BaseModel):
num_warmup: int = Field(2_000, ge=1)
num_samples: int = Field(3_000, ge=1)
num_chains: int = Field(4, ge=1)
inference_params = InferenceParams()
gamma_kernel = NUTS(gamma_model)
gamma_mcmc = MCMC(
gamma_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
gamma_mcmc.run(rng_key, y=censored_gamma_samples)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 0%| | 0/5000 [00:02<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:03<00:00, 1644.63it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:03<00:00, 1648.12it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:03<00:00, 1657.49it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:02<00:00, 1674.47it/s]
我们还生成后验预测样本。
[4]:
gamma_predictive = Predictive(
model=gamma_model, posterior_samples=gamma_mcmc.get_samples()
)
rng_key, rng_subkey = random.split(rng_key)
gamma_posterior_predictive = gamma_predictive(rng_subkey, y=None)
gamma_idata = az.from_numpyro(posterior=gamma_mcmc)
gamma_idata.extend(az.from_numpyro(posterior_predictive=gamma_posterior_predictive))
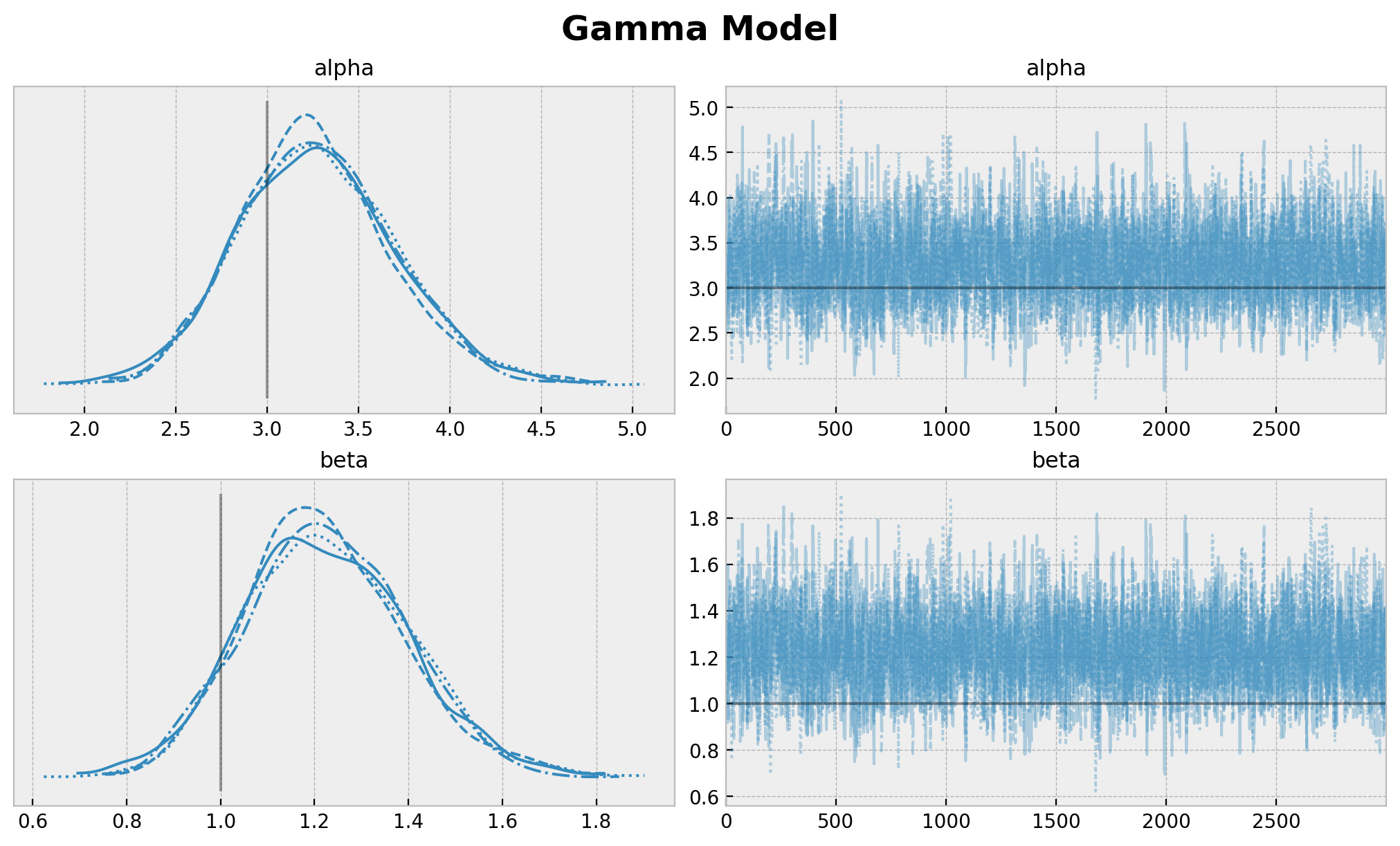
现在我们绘制轨迹,并比较真实参数和估计参数。
[5]:
axes = az.plot_trace(
data=gamma_idata,
compact=True,
lines=[
("alpha", {}, censored_gamma_data_params.alpha),
("beta", {}, censored_gamma_data_params.beta),
],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Gamma Model", fontsize=18, fontweight="bold");
[6]:
axes = az.plot_posterior(
data=gamma_idata,
ref_val=[censored_gamma_data_params.alpha, censored_gamma_data_params.beta],
round_to=3,
figsize=(12, 5),
)
plt.gcf().suptitle("Gamma Model Parameters", fontsize=18, fontweight="bold", y=1.03);
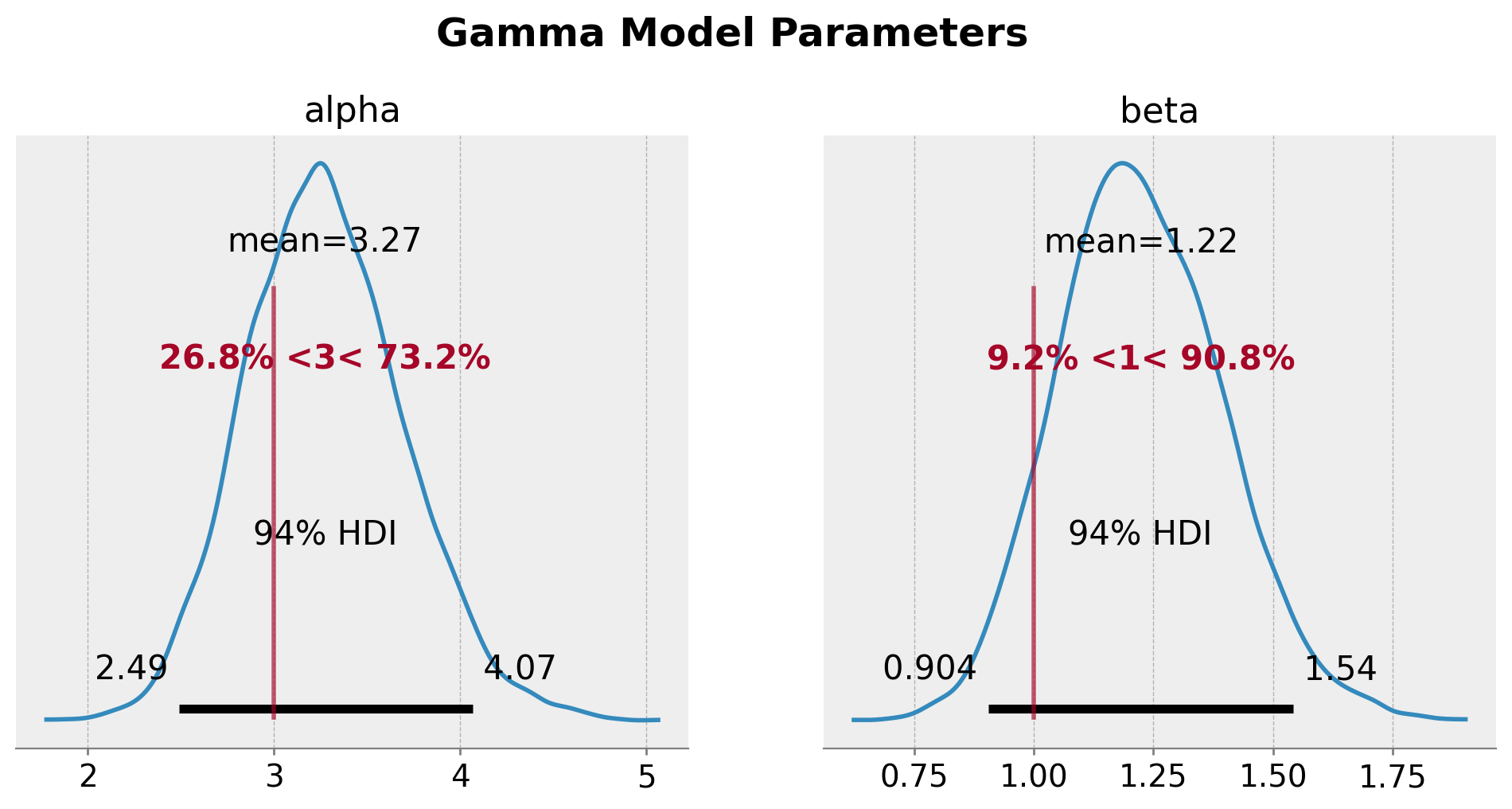
尽管真实参数在 \(94\%\) HDI 范围内,但我们确实看到了参数估计中的偏差。这是预期之中的,因为模型中没有考虑审查。
我们可以可视化推断的分布,并与数据生成过程的真实分布进行比较。
[7]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
gamma_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Gamma Model", fontsize=16, fontweight="bold");
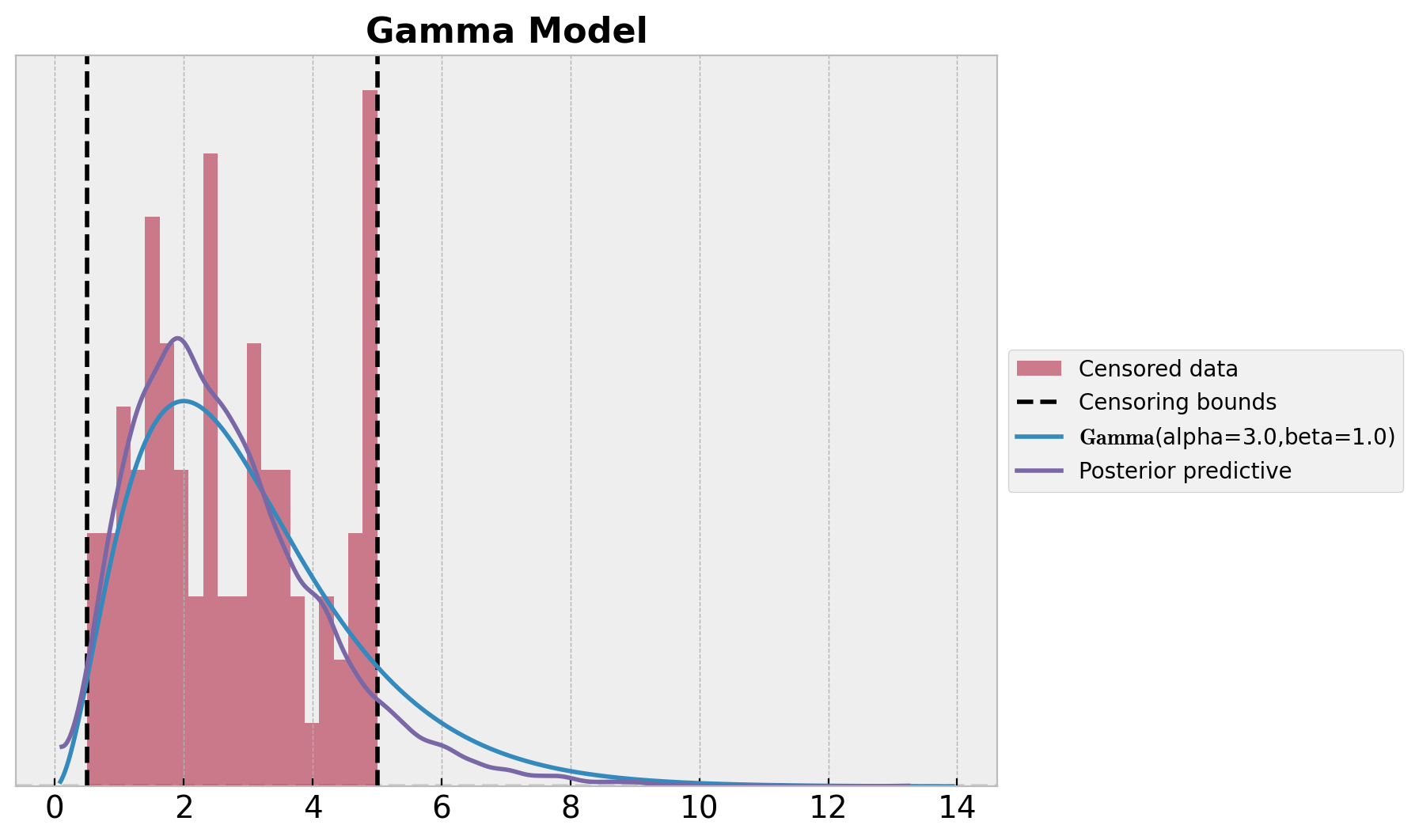
这里可以看到分布匹配得不好。
审查 Gamma 模型
如引言所述,实现审查模型的主要思想是使用 CDF 参数化。原因在于,审查分布的概率密度函数 PDF 是
因此,我们只需将这些条件实现为一个自定义似然函数。为了在 NumPyro 中做到这一点,我们遵循 Uber 博客文章gist中描述的方法。要遵循此策略,我们需要一个指示函数来编码审查
[8]:
def get_truncation_label(y: ArrayImpl, lower: float, upper: float) -> ArrayImpl:
return jnp.where(y == lower, -1, jnp.where(y == upper, 1, 0))
truncation_label = get_truncation_label(
y=censored_gamma_samples,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
)
现在我们准备实现模型。对于区间 \(lower < y < upper\) 内的点,我们直接从 Gamma 分布中采样。另一方面,边界上的点遵循伯努利分布(如果我们对审查掩码值进行建模),其中截断概率可以通过 CDF 进行参数化。我们来看看具体如何操作
[9]:
def censored_gamma_model(
y: ArrayImpl, lower: float, upper: float, truncation_label: ArrayImpl
) -> None:
alpha = numpyro.sample("alpha", dist.Exponential(1.0))
beta = numpyro.sample("beta", dist.Exponential(1.0))
distribution = dist.Gamma(concentration=alpha, rate=beta)
with mask(mask=truncation_label == -1):
truncation_prob_lower = distribution.cdf(lower)
numpyro.sample(
"truncated_label_lower", dist.Bernoulli(truncation_prob_lower), obs=1
)
with mask(mask=truncation_label == 0):
numpyro.sample("obs", distribution, obs=y)
with mask(mask=truncation_label == 1):
truncation_prob_upper = 1 - distribution.cdf(upper)
numpyro.sample(
"truncated_label_upper", dist.Bernoulli(truncation_prob_upper), obs=1
)
[10]:
censored_gamma_kernel = NUTS(censored_gamma_model)
censored_gamma_mcmc = MCMC(
censored_gamma_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_mcmc.run(
rng_key,
y=censored_gamma_samples,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
truncation_label=truncation_label,
)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:04<00:00, 1028.68it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:04<00:00, 1029.09it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:04<00:00, 1029.55it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:04<00:00, 1030.11it/s]
备注:请注意,很容易为模型添加下方和上方审查成分(Uber 的博客文章只有一个审查成分)。
现在我们拟合模型并评估结果
[11]:
censored_gamma_predictive = Predictive(
model=censored_gamma_model,
posterior_samples=censored_gamma_mcmc.get_samples(),
return_sites=["obs"],
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_posterior_predictive = censored_gamma_predictive(
rng_subkey,
y=None,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
truncation_label=truncation_label,
)
censored_gamma_idata = az.from_numpyro(posterior=censored_gamma_mcmc)
censored_gamma_idata.extend(
az.from_numpyro(posterior_predictive=censored_gamma_posterior_predictive)
)
[12]:
axes = az.plot_trace(
data=censored_gamma_idata,
compact=True,
lines=[
("alpha", {}, censored_gamma_data_params.alpha),
("beta", {}, censored_gamma_data_params.beta),
],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Censored Gamma Model", fontsize=18, fontweight="bold");
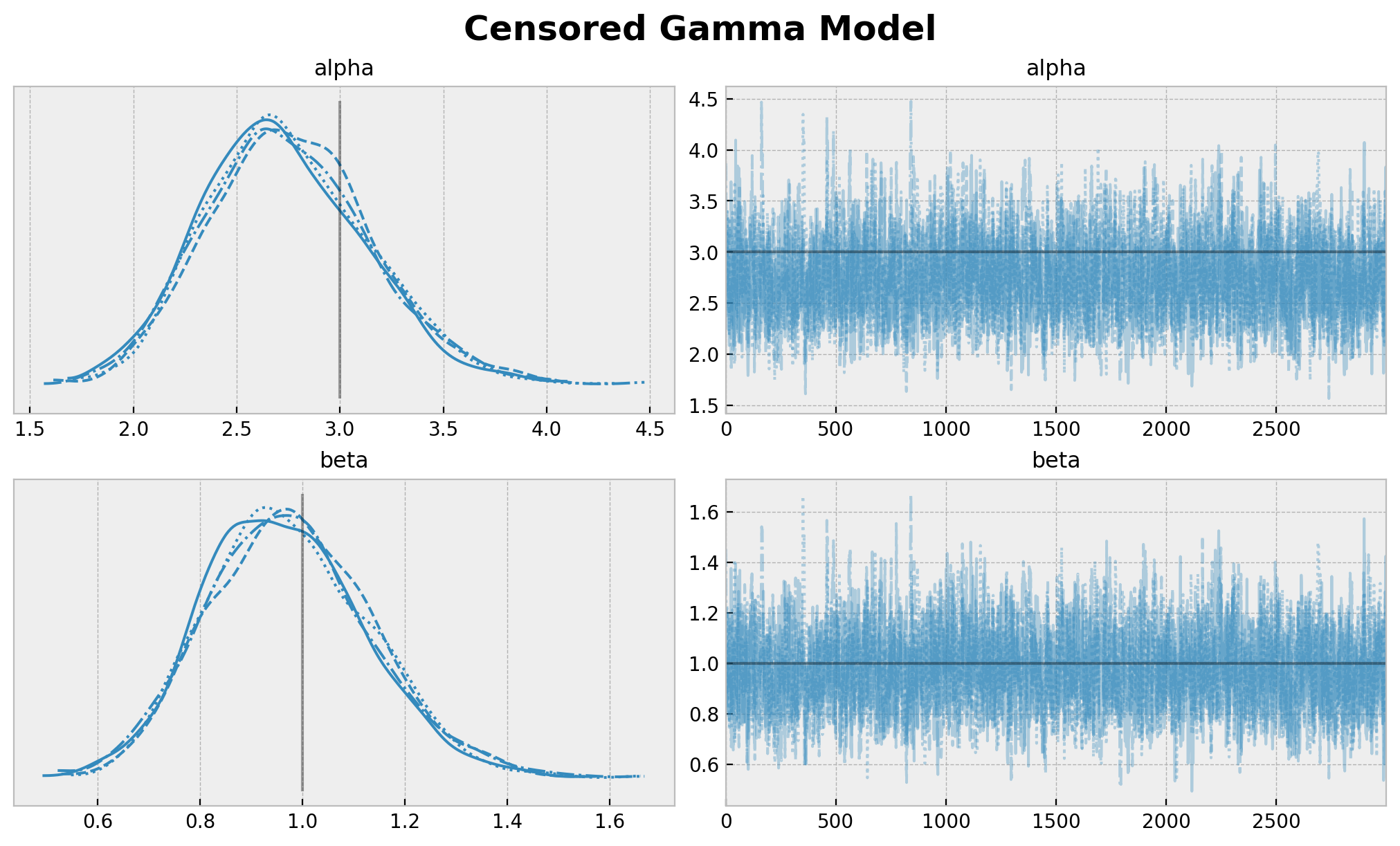
[13]:
axes = az.plot_posterior(
data=censored_gamma_idata,
ref_val=[censored_gamma_data_params.alpha, censored_gamma_data_params.beta],
round_to=3,
figsize=(12, 5),
)
plt.gcf().suptitle(
"Censored Gamma Model Parameters", fontsize=18, fontweight="bold", y=1.03
);
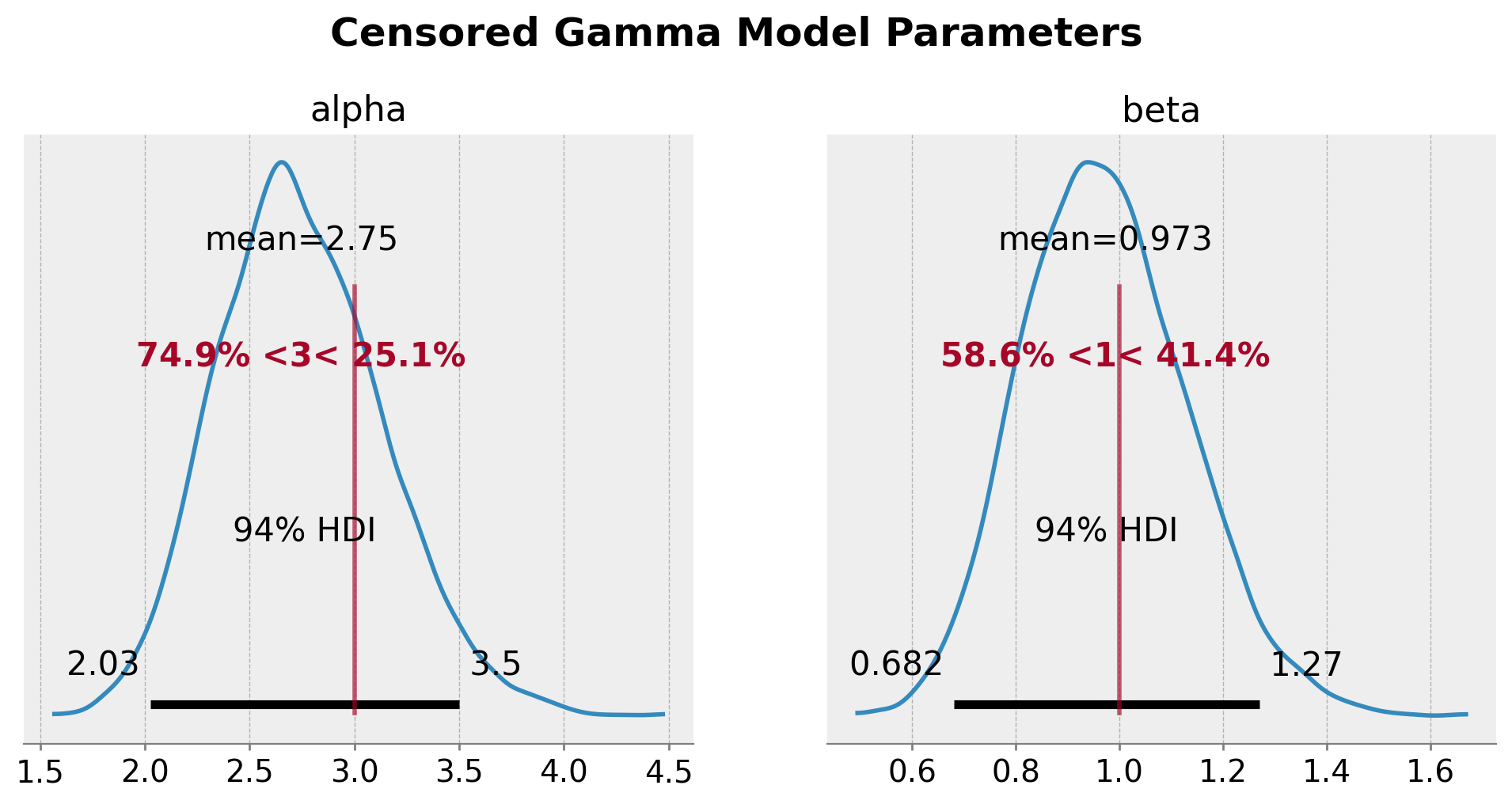
我们清楚地看到,真实参数与后验分布的均值和众数相符。审查模型能够恢复真实参数。
就像对朴素模型所做的那样,我们可视化推断的分布,并与数据生成过程的真实分布进行比较。
[14]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
censored_gamma_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Gamma Model (no clipping)", fontsize=16, fontweight="bold");
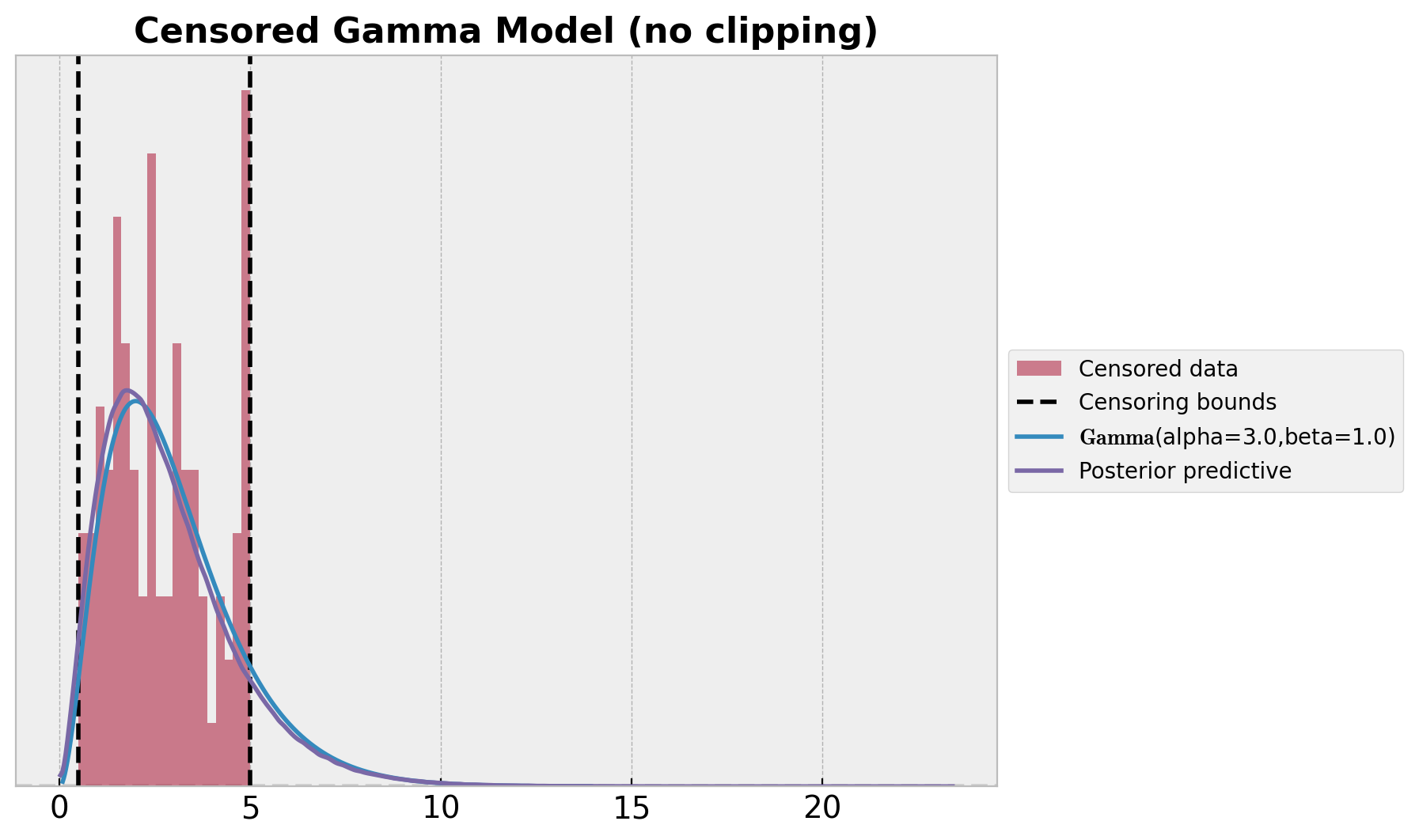
这看起来比朴素模型好得多。然而,这里有些问题,因为我们只从 obs 变量中采样!我们不应该有超出审查界限的后验样本。通过将样本裁剪到界限内,我们可以轻松解决这个问题。
[15]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
censored_gamma_idata["posterior_predictive"]["obs"]
.clip(min=censored_gamma_data_params.lower, max=censored_gamma_data_params.upper)
.to_numpy()
.flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Gamma Model", fontsize=16, fontweight="bold");
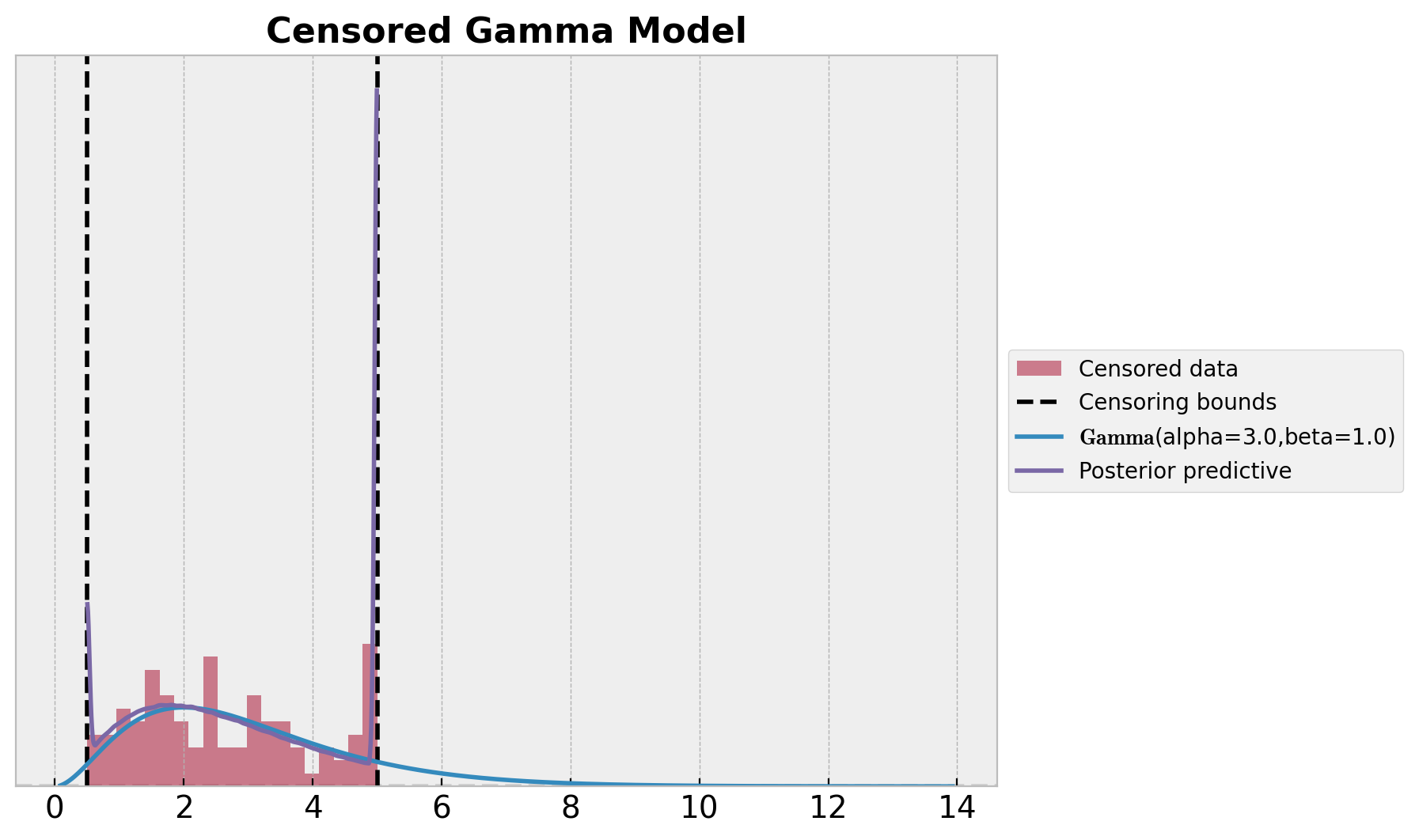
第二部分:离散分布
在第二部分中,我们进行的操作与第一部分相同,但针对离散分布。同样,我们假设有一个观测值数据集 \(y\),它们在已知阈值处被从下方和上方审查。这次我们假设数据遵循泊松分布(参数为 \(\lambda\))。我们希望恢复真实参数 \(\lambda\)。审查模型结构与连续情况相同,但在上限处有一个小细节。我们需要在截断概率中添加一项,以考虑上限的概率。具体来说,我们需要使用 PDF 添加上限的概率。
生成审查数据
我们从泊松分布生成数据,并将其裁剪至阈值 lower 和 upper 之间。然后绘制数据的直方图和真实的泊松分布。
[16]:
class CensoredPoissonDataParams(BaseModel):
rate: float = Field(..., description="Rate parameter", gt=0)
lower: float = Field(..., description="Lower censoring bound", gt=0)
upper: float = Field(..., description="Upper censoring bound", gt=0)
n: int = Field(..., description="Number of samples", gt=0)
def generate_censored_poisson_samples(
rng_key: ArrayImpl, params: CensoredPoissonDataParams
) -> ArrayImpl:
raw_samples = dist.Poisson(rate=params.rate).sample(rng_key, (params.n,))
return jnp.clip(raw_samples, params.lower, params.upper)
censored_poisson_data_params = CensoredPoissonDataParams(
rate=1, lower=1, upper=4, n=100
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_samples = generate_censored_poisson_samples(
rng_key=rng_subkey, params=censored_poisson_data_params
)
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
align="left",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
ax.set_title("Censored Poisson Sample Data", fontsize=16, fontweight="bold");
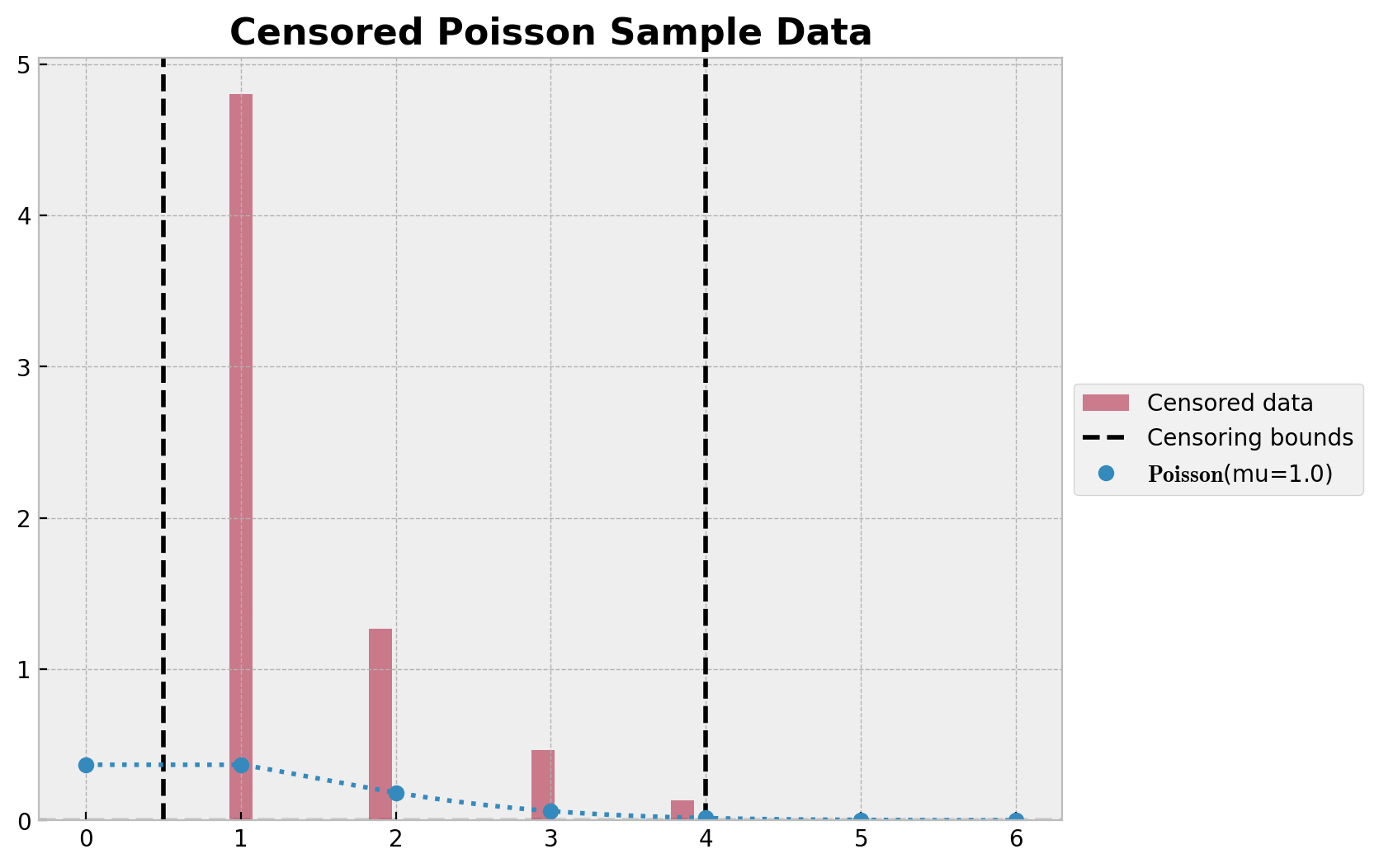
朴素模型
就像连续情况一样,我们从一个不考虑审查成分的朴素模型开始。我们只使用具有参数 \(\lambda\) 的泊松分布对数据进行建模。
[17]:
def poisson_model(y: ArrayImpl) -> None:
rate = numpyro.sample("rate", dist.Exponential(1.0))
numpyro.sample("obs", dist.Poisson(rate), obs=y)
poisson_kernel = NUTS(poisson_model)
poisson_mcmc = MCMC(
poisson_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
poisson_mcmc.run(rng_key, y=censored_poisson_samples)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:02<00:00, 2123.00it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:02<00:00, 2126.03it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:02<00:00, 2129.97it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:02<00:00, 2134.66it/s]
[18]:
poisson_predictive = Predictive(
model=poisson_model, posterior_samples=poisson_mcmc.get_samples()
)
rng_key, rng_subkey = random.split(rng_key)
poisson_posterior_predictive = poisson_predictive(rng_subkey, y=None)
poisson_idata = az.from_numpyro(posterior=poisson_mcmc)
poisson_idata.extend(az.from_numpyro(posterior_predictive=poisson_posterior_predictive))
[19]:
axes = az.plot_trace(
data=poisson_idata,
compact=True,
lines=[("rate", {}, censored_poisson_data_params.rate)],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Poisson Model", fontsize=18, fontweight="bold");
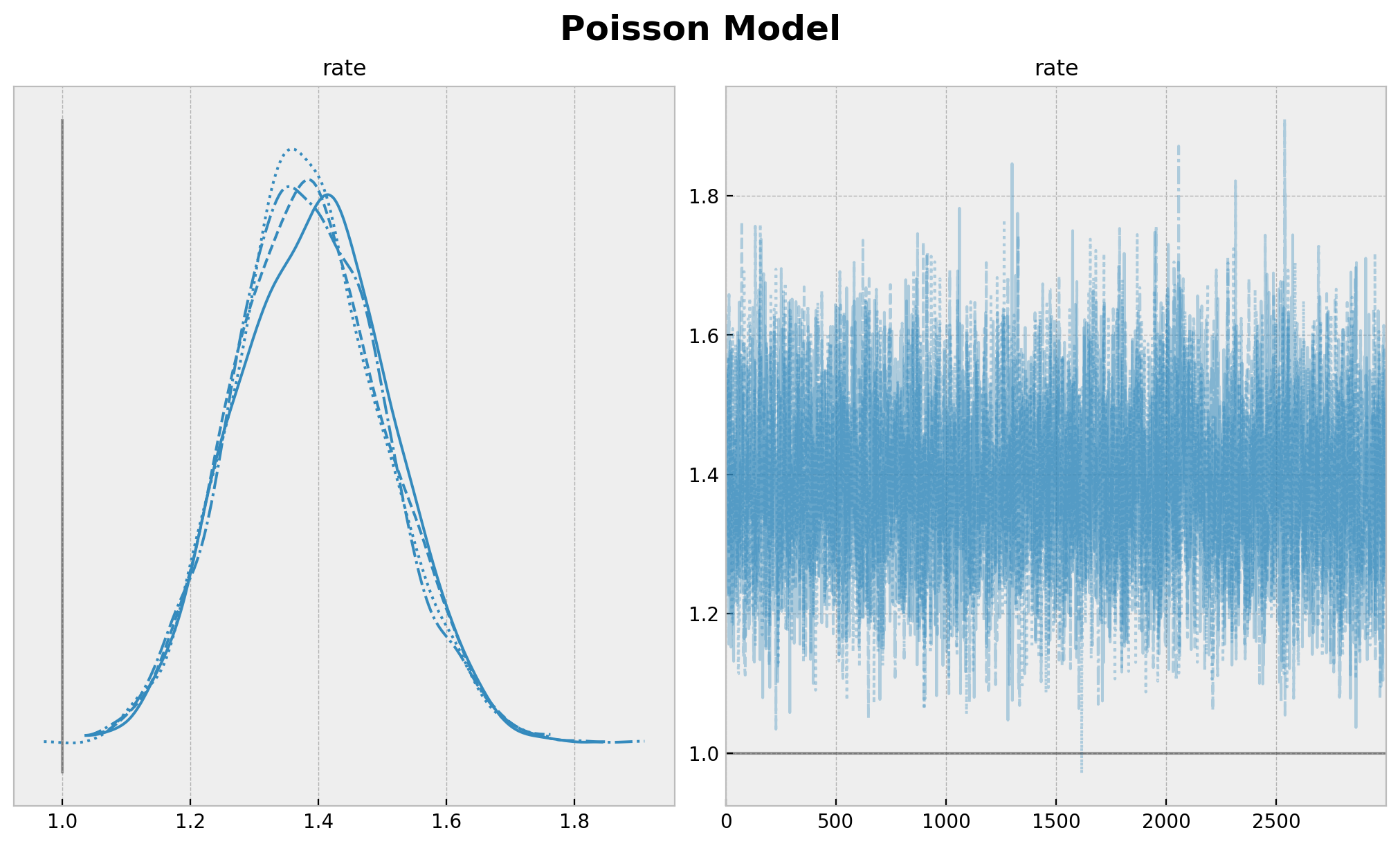
[20]:
axes = az.plot_posterior(
data=poisson_idata,
ref_val=[censored_poisson_data_params.rate],
round_to=3,
figsize=(10, 6),
)
plt.gcf().suptitle("Poisson Model Parameter", fontsize=18, fontweight="bold");
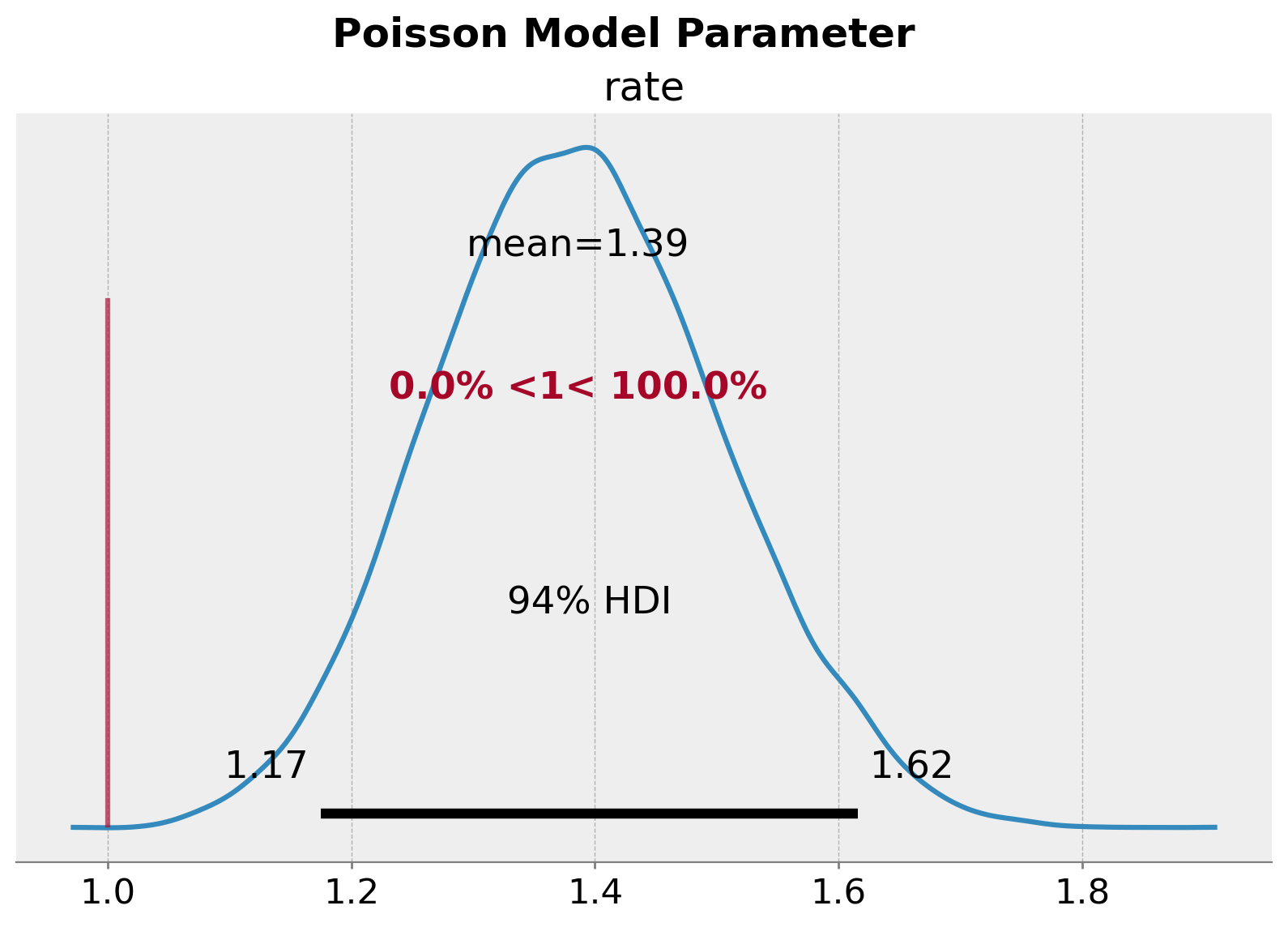
我们清楚地看到参数估计中的偏差。率参数 \(\lambda\) 的真实值甚至不在 \(94\%\) HDI 范围内。
我们还可以看看后验预测分布。
[21]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
poisson_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
bins=50,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Poisson Model", fontsize=16, fontweight="bold");
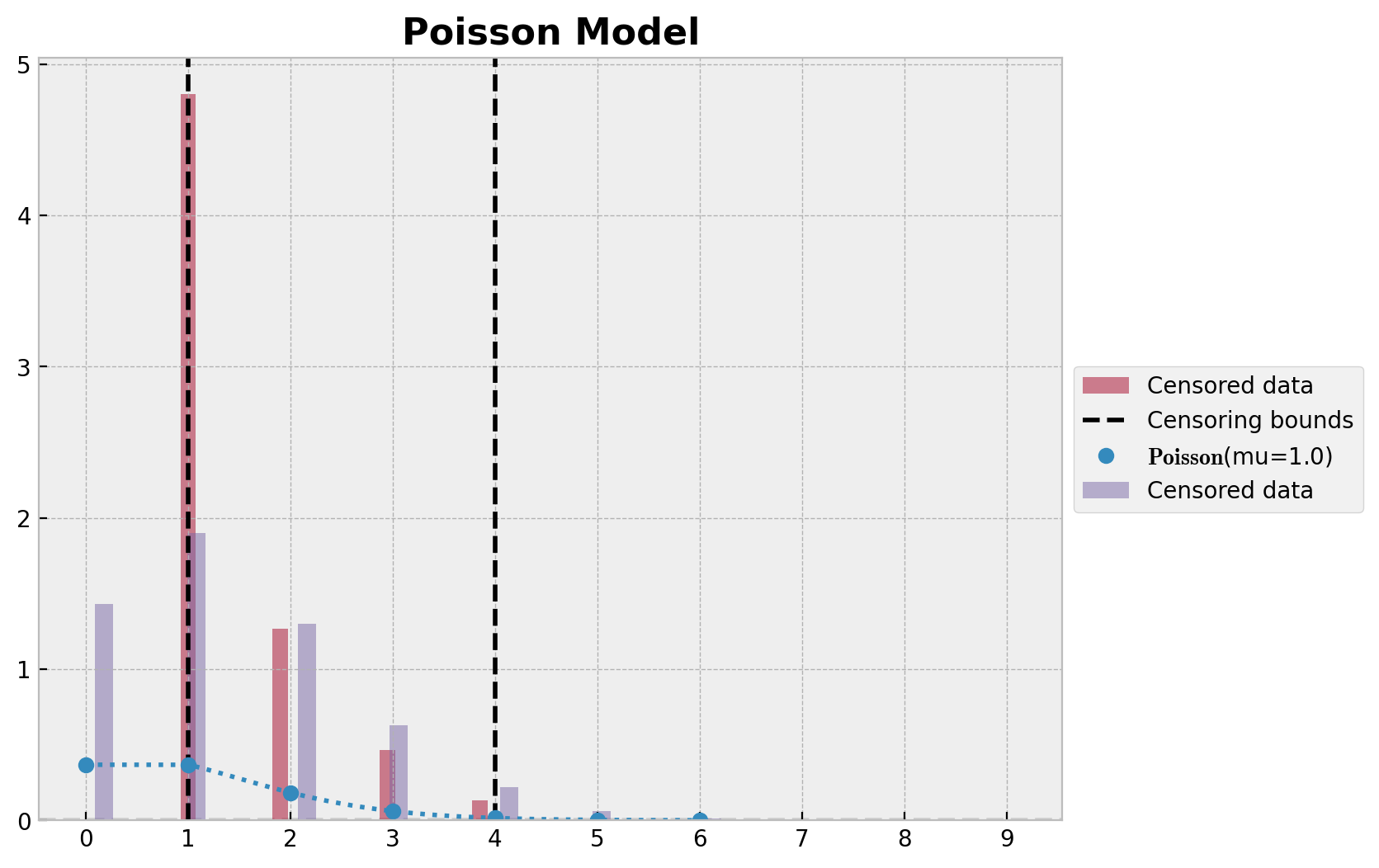
审查泊松模型
现在我们来处理审查模型。和之前一样,我们需要获取审查标签来管理似然成分
[22]:
truncation_label = get_truncation_label(
y=censored_poisson_samples,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
)
现在,最后关于上方审查成分的细节。
我们想要考虑封闭区间 \(P(lower \leq y \leq upper)\)。
对于上方区间,我们使用 \(1 - CDF(upper) = 1- P(y \leq upper) = P(y > upper)\),但我们实际需要 \((P \geq upper)\)。
因此,我们需要在上方截断概率中加上 \(P(y= upper)\)。
请注意,对于连续情况,此讨论无关紧要,因为单个点的概率为零,所以 \(P(y > upper) = P(y \geq upper)\)。
模型的实现现在应该更清晰了。
[23]:
def censored_poisson_model(
y: ArrayImpl, lower: float, upper: float, truncation_label: ArrayImpl
) -> None:
rate = numpyro.sample("rate", dist.Exponential(1.0))
distribution = dist.Poisson(rate)
with mask(mask=truncation_label == -1):
truncation_prob_lower = distribution.cdf(lower)
numpyro.sample(
"truncated_label_lower", dist.Bernoulli(truncation_prob_lower), obs=1
)
with mask(mask=truncation_label == 0):
numpyro.sample("obs", distribution, obs=y)
with mask(mask=truncation_label == 1):
ccdf_upper = 1 - distribution.cdf(upper)
pmf_upper = jnp.exp(distribution.log_prob(upper))
truncation_prob_upper = ccdf_upper + pmf_upper
numpyro.sample(
"truncated_label_upper", dist.Bernoulli(truncation_prob_upper), obs=1
)
备注:这是 Kyle Caron 在其博客文章“用第一性原理建模一切:极端缺货下的需求”中指出的一个重要细节。
我们继续拟合模型,并将结果与真实参数进行比较。
[24]:
censored_poisson_kernel = NUTS(censored_poisson_model)
censored_poisson_mcmc = MCMC(
censored_poisson_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_mcmc.run(
rng_key,
y=censored_poisson_samples,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
truncation_label=truncation_label,
)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:03<00:00, 1257.60it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:03<00:00, 1259.63it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:03<00:00, 1260.75it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:03<00:00, 1261.95it/s]
[25]:
censores_poisson_predictive = Predictive(
model=censored_poisson_model,
posterior_samples=censored_poisson_mcmc.get_samples(),
return_sites=["obs"],
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_posterior_predictive = censores_poisson_predictive(
rng_subkey,
y=None,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
truncation_label=truncation_label,
)
censored_poisson_idata = az.from_numpyro(posterior=censored_poisson_mcmc)
censored_poisson_idata.extend(
az.from_numpyro(posterior_predictive=censored_poisson_posterior_predictive)
)
[26]:
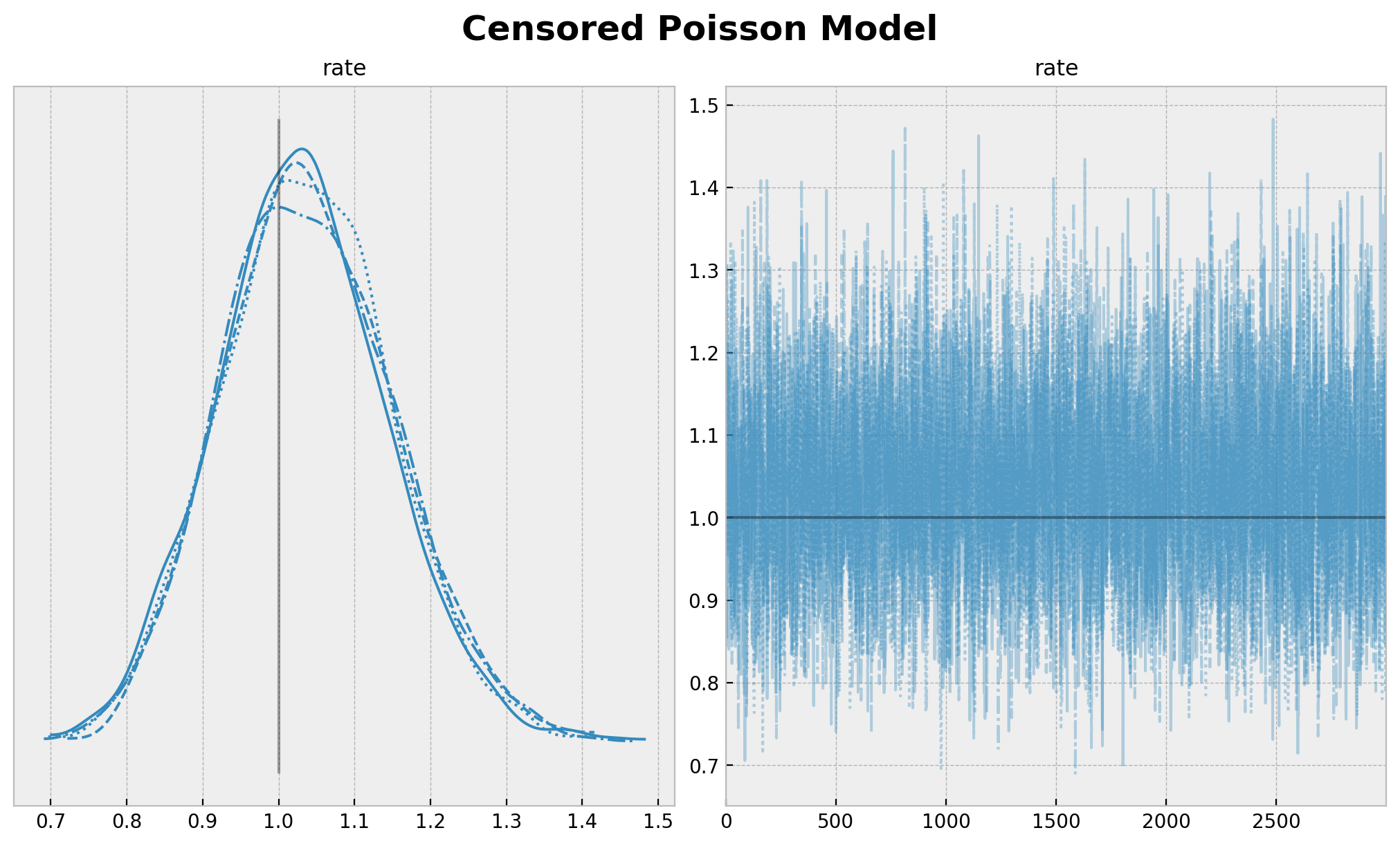
axes = az.plot_trace(
data=censored_poisson_idata,
compact=True,
lines=[("rate", {}, censored_poisson_data_params.rate)],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Censored Poisson Model", fontsize=18, fontweight="bold");
[27]:
axes = az.plot_posterior(
data=censored_poisson_idata,
ref_val=[censored_poisson_data_params.rate],
round_to=3,
figsize=(10, 6),
)
plt.gcf().suptitle("Censored Poisson Model Parameter", fontsize=18, fontweight="bold");
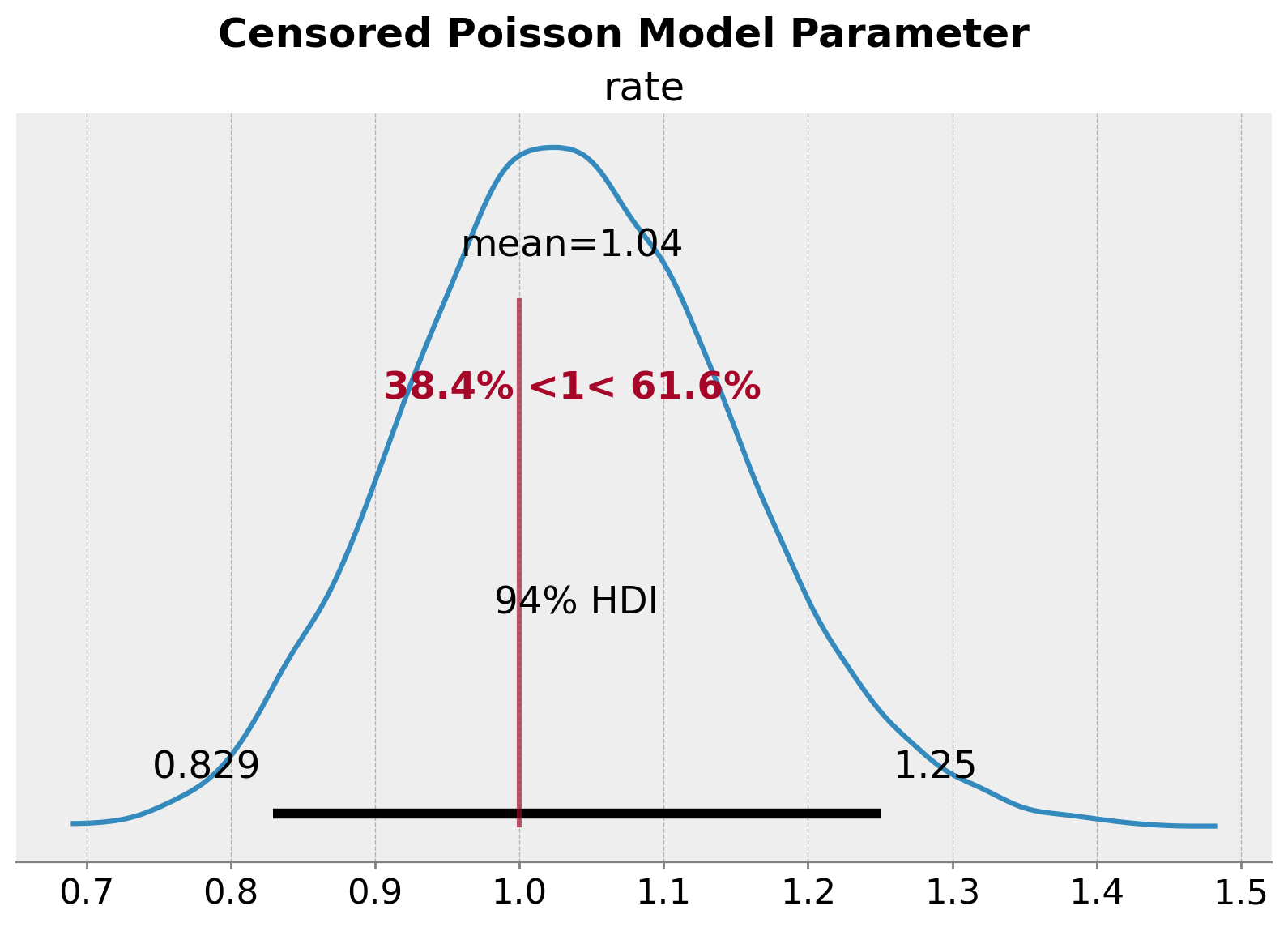
我们看到我们已经恢复了率参数 \(\lambda = 1\) 的真实值。
这是后验预测分布
[28]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
censored_poisson_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
bins=50,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Poisson Model (no clipping)", fontsize=16, fontweight="bold");
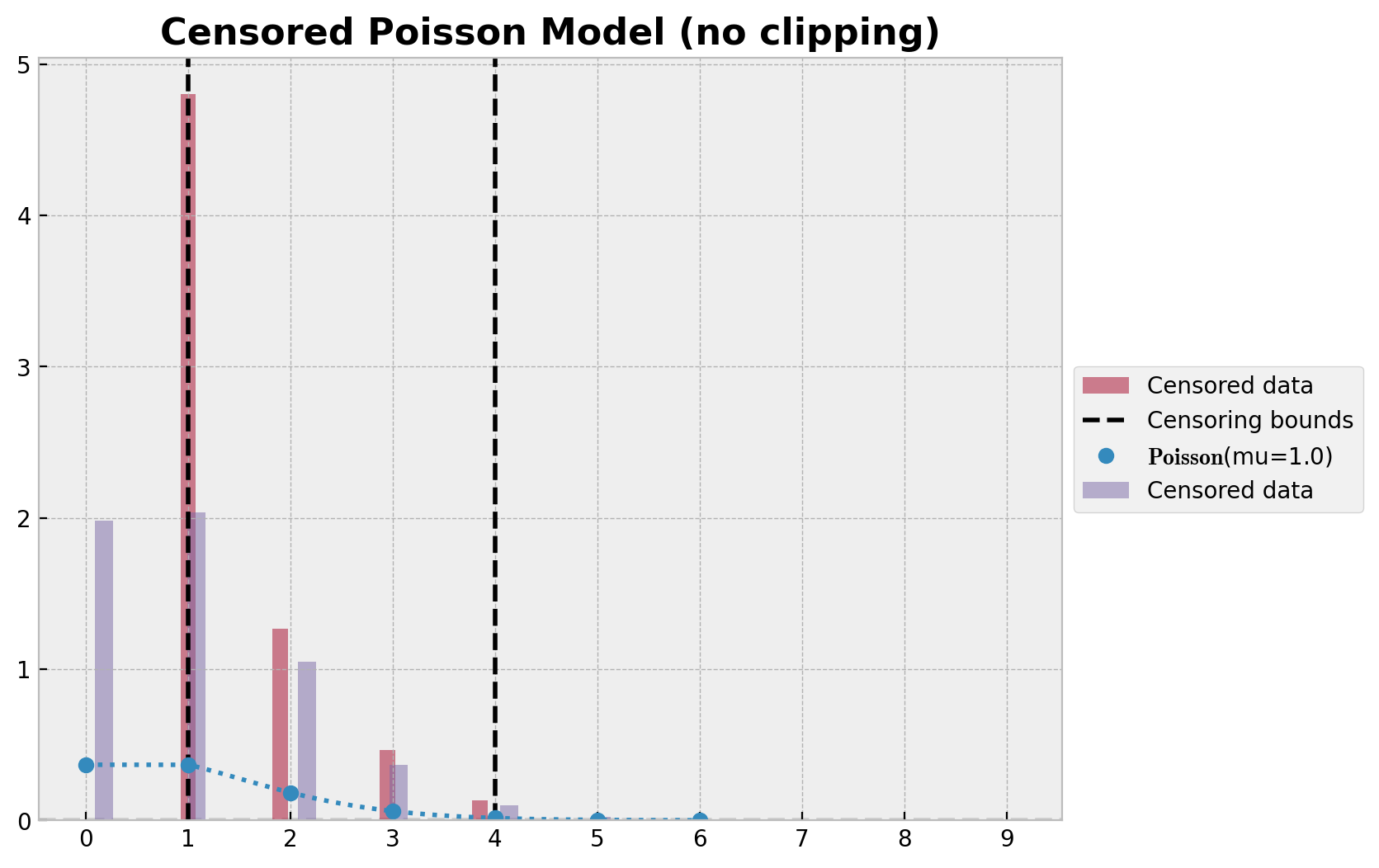
如前所述,为了获得正确的后验预测分布,我们需要将样本裁剪到界限内。
[29]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
censored_poisson_idata["posterior_predictive"]["obs"]
.clip(
min=censored_poisson_data_params.lower, max=censored_poisson_data_params.upper
)
.to_numpy()
.flatten(),
bins=20,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Poisson Model", fontsize=16, fontweight="bold");
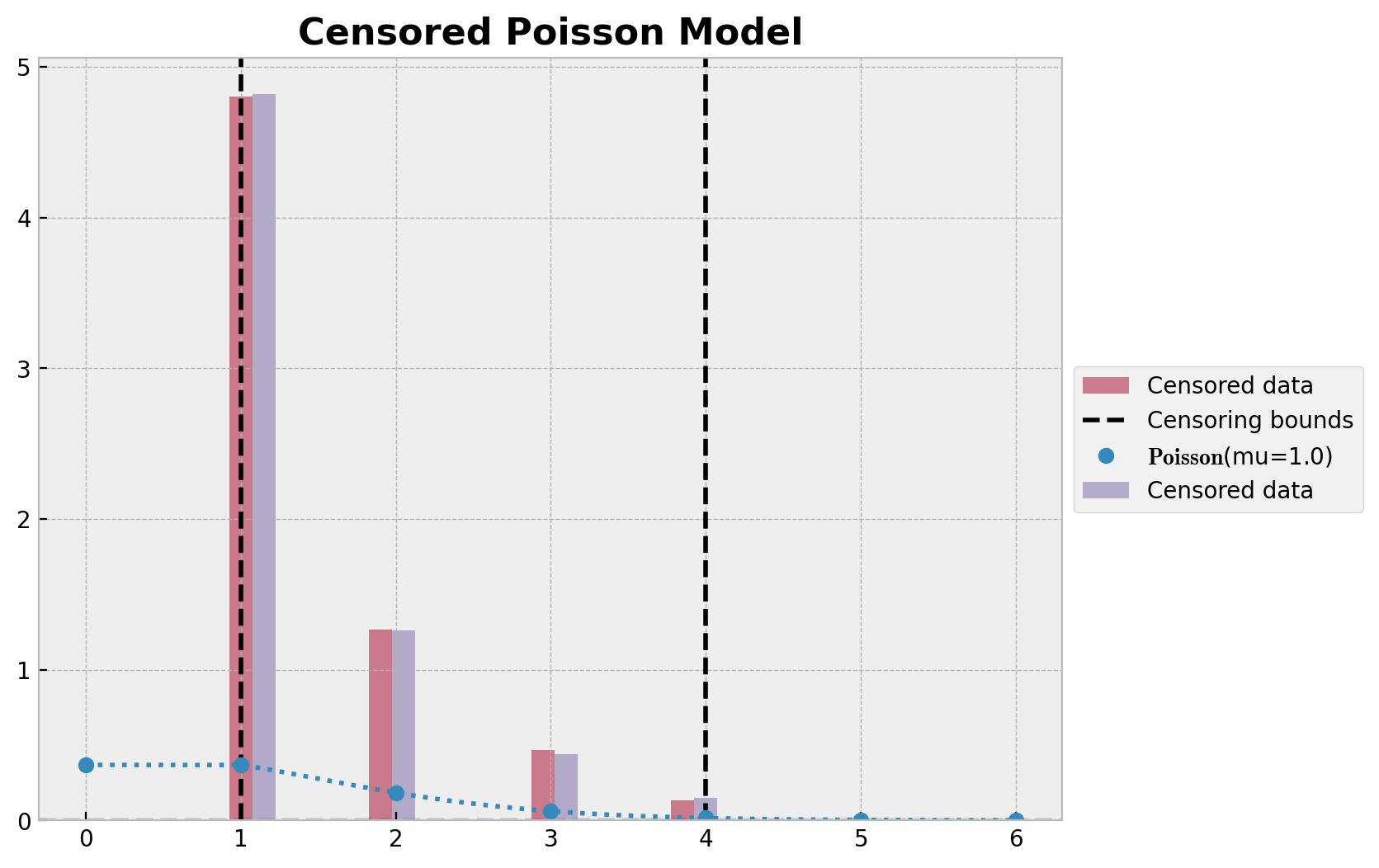
在这里我们看到观测分布和预测分布匹配得很好。