交互式在线版本：

NumPyro 与其他库的集成

在本 Notebook 中，我们将介绍如何将 NumPyro 与其他库集成，以利用替代的推断算法。我们重点关注两个库

• Blackjax

  • 我们考虑 Pathfinder 变分推断算法。

• FlowMC

  • 我们研究正则化流增强的马尔可夫链蒙特卡洛方法。

集成的核心思想是使用函数 numpyro.infer.util.initialize_model 来计算对数密度以及从无约束空间到约束空间所需的变换。让我们看看如何实现。

此示例基于原始示例 Notebook NumPyro with Pathfinder。

准备 Notebook

!pip install -q numpyro@git+https://github.com/pyro-ppl/numpyro arviz blackjax flowMC

import arviz as az
import blackjax
from flowMC.nfmodel.rqSpline import MaskedCouplingRQSpline
from flowMC.proposal.MALA import MALA
from flowMC.Sampler import Sampler
import matplotlib.pyplot as plt
import numpy as np

import jax
from jax import random

import numpyro
import numpyro.distributions as dist
from numpyro.infer.util import Predictive, initialize_model

plt.style.use("bmh")

plt.rcParams["figure.figsize"] = [10, 6]
plt.rcParams["figure.dpi"] = 100
plt.rcParams["figure.facecolor"] = "white"

jax.config.update("jax_enable_x64", True)

numpyro.set_host_device_count(n=4)

rng_key = random.PRNGKey(seed=42)

assert numpyro.__version__.startswith("0.18.0")

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"

生成合成数据

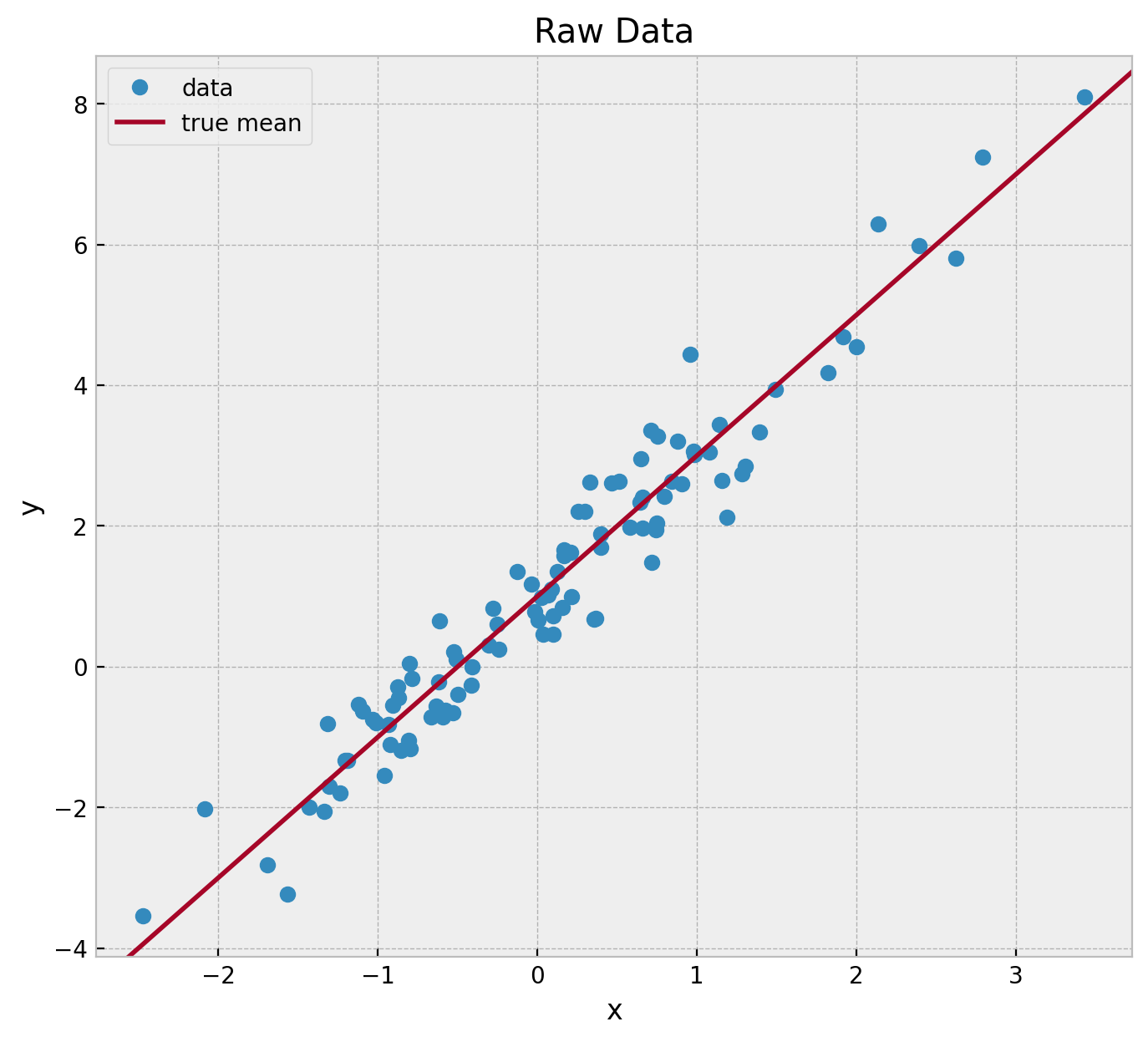
我们从一个简单的线性回归模型生成一些数据。

def generate_data(rng_key, a, b, sigma, n):
    x = random.normal(rng_key, (n,))
    rng_key, rng_subkey = random.split(rng_key)
    epsilon = sigma * random.normal(rng_subkey, (n,))
    y = a + b * x + epsilon
    return x, y


# true parameters
a = 1.0
b = 2.0
sigma = 0.5
n = 100

# generate data
rng_key, rng_subkey = random.split(rng_key)
x, y = generate_data(rng_key, a, b, sigma, n)

# plot data
fig, ax = plt.subplots(figsize=(8, 7))
ax.plot(x, y, "o", c="C0", label="data")
ax.axline((0, a), slope=b, color="C1", label="true mean")
ax.legend(loc="upper left")
ax.set(xlabel="x", ylabel="y", title="Raw Data");

模型规范

我们在 NumPyro 中定义一个简单的线性回归模型。

def model(x, y=None):
    a = numpyro.sample("a", dist.Normal(loc=0.0, scale=2.0))
    b = numpyro.sample("b", dist.HalfNormal(scale=2.0))
    sigma = numpyro.sample("sigma", dist.Exponential(rate=1.0))
    mean = numpyro.deterministic("mu", a + b * x)
    with numpyro.plate("data", len(x)):
        numpyro.sample("likelihood", dist.Normal(loc=mean, scale=sigma), obs=y)


numpyro.render_model(
    model=model,
    model_args=(x, y),
    render_distributions=True,
    render_params=True,
)

提取模型要素

如引言所述，我们需要使用函数 numpyro.infer.util.initialize_model 来提取 Blackjax 和 FlowMC 所需的对数密度以及从无约束空间到约束空间的必要变换。此函数的输入是模型、数据和一个随机键。

rng_key, rng_subkey = random.split(rng_key)
param_info, potential_fn, postprocess_fn, *_ = initialize_model(
    rng_subkey,
    model,
    model_args=(x, y),
    dynamic_args=True,  # <- this is important!
)

• param_info 是一个名为 ParamInfo 的具名元组 (namedtuple)，包含用于启动 MCMC 的先验分布中的值。

• potential_fn 是一个可调用对象，根据数据和参数返回模型的势能。

• postprocess_fn 是一个可调用对象，它使用逆变换将无约束的 HMC 样本转换为位于 site 支持范围内的约束值，此外还返回模型中确定性 site 的值。

让我们从参数中提取一个初始位置。

# get initial position
initial_position = param_info.z
initial_position

{'a': Array(-1.5517484, dtype=float64),
 'b': Array(1.12366214, dtype=float64),
 'sigma': Array(-0.52973833, dtype=float64)}

注意 观察到 sigma 的初始位置是负数。原因是 sigma 的先验分布是 dist.Exponential(rate=1.0)，这是一个正分布。因此，我们需要通过双射变换将其转换为无约束空间。函数 postprocess_fn 将使用逆变换将这个负值转换为正空间。

接下来，我们将势能函数转换为对数密度函数。

# get log-density from the potential function
def logdensity_fn(position):
    func = potential_fn(x, y)
    return -func(position)

让我们验证我们可以在初始位置评估对数密度函数。

logdensity_fn(initial_position)

Array(-1141.81434653, dtype=float64)

现在，我们准备好运行我们的第一个采样器了。

Pathfinder 采样器

来自 Blackjax 文档

Pathfinder 沿拟牛顿优化路径定位目标密度的正态逼近，其中局部协方差使用 L-BFGS 优化器产生的逆 Hessian 估计值进行估计。PathfinderState 存储 L-BFGS 优化器迭代的结果 ELBO 和从近似目标密度中采样所需的所有因子。

有关 Pathfinder 的更多信息，请参阅此论文

Lu Zhang, Bob Carpenter, Andrew Gelman, and Aki Vehtari.Pathfinder: parallel quasi-newton variational inference. Journal of Machine Learning Research, 23(306):1–49, 2022.

注意： 来自 Blackjax 采样手册文档

L-BFGS 算法在处理 float32 和对数似然函数时存在困难；建议使用双精度浮点数。

运行采样器

我们现在可以使用 blackjax.vi.pathfinder.approximate 来运行变分推断算法。

%%time

# run pathfinder
rng_key, rng_subkey = random.split(rng_key)
pathfinder_state, _ = blackjax.vi.pathfinder.approximate(
    rng_key=rng_subkey,
    logdensity_fn=logdensity_fn,
    initial_position=initial_position,
    num_samples=15_000,
    ftol=1e-4,
)

# sample from the posterior
rng_key, rng_subkey = random.split(rng_key)
posterior_samples_pathfinder, _ = blackjax.vi.pathfinder.sample(
    rng_key=rng_subkey,
    state=pathfinder_state,
    num_samples=5_000,
)

# convert to arviz
idata_pathfinder = az.from_dict(
    posterior={
        k: np.expand_dims(a=np.asarray(v), axis=0)
        for k, v in posterior_samples_pathfinder.items()
    },
)

CPU times: user 2.59 s, sys: 278 ms, total: 2.87 s
Wall time: 2.55 s

可视化结果

我们可以在采样后可视化结果。

az.summary(data=idata_pathfinder, round_to=3)

arviz - WARNING - Shape validation failed: input_shape: (1, 5000), minimum_shape: (chains=2, draws=4)

	均值	标准差	hdi_3%	hdi_97%	mcse_均值	mcse_标准差	ess_bulk	ess_tail	r_hat
a	0.973	0.052	0.878	1.070	0.001	0.001	4882.712	4860.828	NaN
b	0.684	0.022	0.645	0.726	0.000	0.000	4797.817	4793.793	NaN
sigma	-0.632	0.063	-0.753	-0.515	0.001	0.001	4723.374	4790.730	NaN

axes = az.plot_trace(
    data=idata_pathfinder,
    compact=True,
    figsize=(10, 6),
    backend_kwargs={"layout": "constrained"},
)
plt.gcf().suptitle(
    t="Pathfinder Trace - Transformed Space", fontsize=18, fontweight="bold"
);

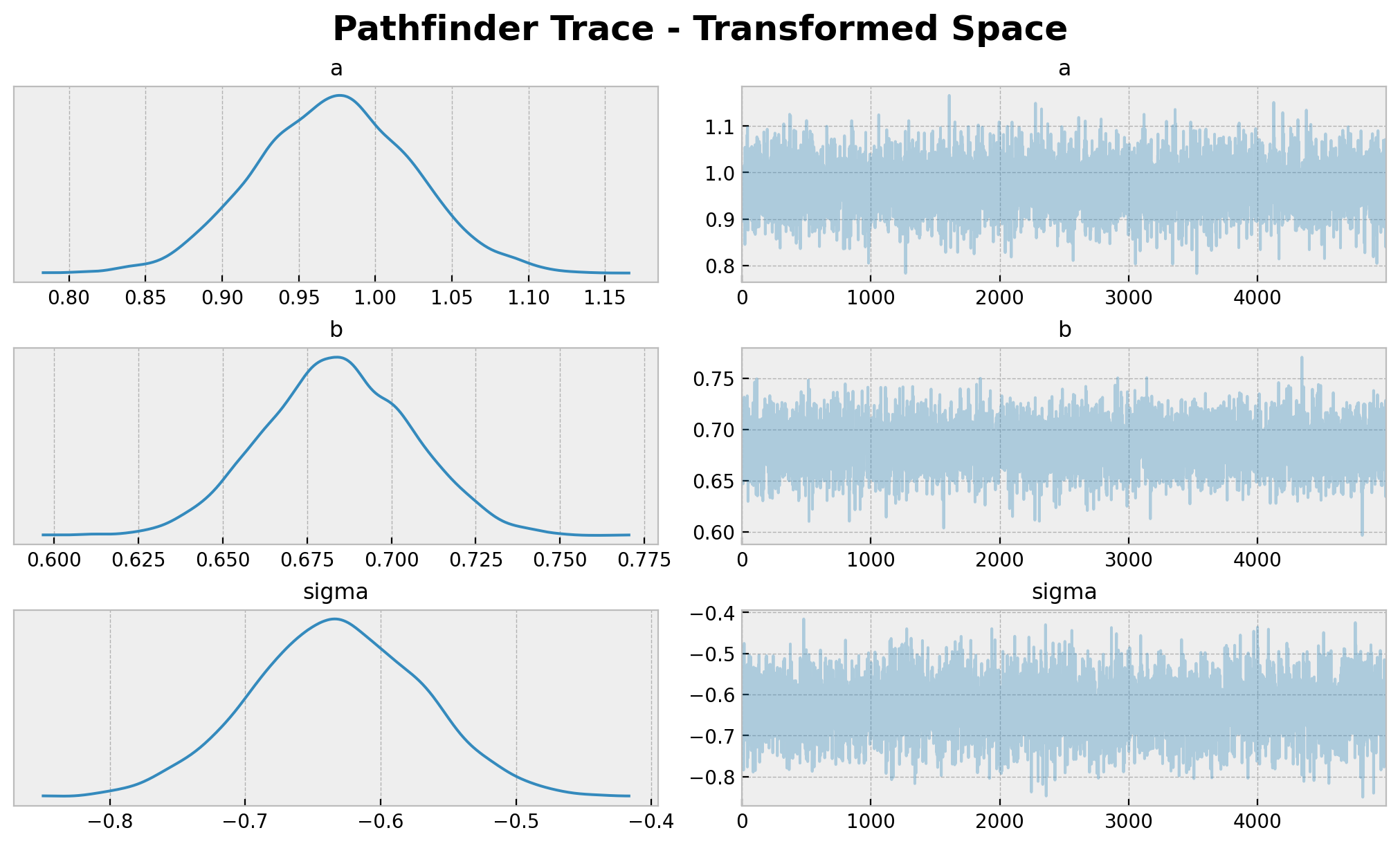
请注意，a 的值接近真实值 1.0。然而，b 和 sigma 的值分别与真实值 2.0 和 0.5 不符。同样，原因在于我们是在无约束空间中进行计算。我们需要将样本转换回原始空间，才能与真实值进行比较。

转换样本

我们可以使用 initialize_model 返回的 postprocess_fn 函数，将样本从无约束空间转换到约束空间

# posterior samples
posterior_samples_pathfinder_transformed = jax.vmap(postprocess_fn(x, y))(
    posterior_samples_pathfinder
)

# posterior predictive samples
rng_key, rng_subkey = random.split(rng_key)
posterior_predictive_samples_pathfinder_transformed = Predictive(
    model=model, posterior_samples=posterior_samples_pathfinder_transformed
)(rng_subkey, x)

让我们看看原始空间中的后验分布。

idata_pathfinder_transformed = az.from_dict(
    posterior={
        k: np.expand_dims(a=np.asarray(v), axis=0)
        for k, v in posterior_samples_pathfinder_transformed.items()
    },
    posterior_predictive={
        k: np.expand_dims(a=np.asarray(v), axis=0)
        for k, v in posterior_predictive_samples_pathfinder_transformed.items()
    },
)

axes = az.plot_trace(
    data=idata_pathfinder_transformed,
    var_names=["~mu"],
    compact=True,
    figsize=(10, 6),
    lines=[
        ("a", {}, a),
        ("b", {}, b),
        ("sigma", {}, sigma),
    ],
    backend_kwargs={"layout": "constrained"},
)
plt.gcf().suptitle(
    t="Pathfinder Trace - Original Space", fontsize=18, fontweight="bold"
);

最后，我们可以可视化后验预测分布。

fig, ax = plt.subplots(figsize=(7, 6))
ax.plot(x, y, "o", c="C0", label="data")
ax.axline((0, a), slope=b, color="C1", label="true mean")
az.plot_hdi(
    x=x,
    y=idata_pathfinder_transformed["posterior_predictive"]["mu"],
    color="C2",
    fill_kwargs={"alpha": 0.7, "label": "mu posterior ($94\\%$ HDI)"},
    ax=ax,
)
az.plot_hdi(
    x=x,
    y=idata_pathfinder_transformed["posterior_predictive"]["likelihood"],
    color="C2",
    fill_kwargs={"alpha": 0.2, "label": "posterior predictive ($94\\%$ HDI)"},
    ax=ax,
)
ax.legend(loc="upper left")
ax.set(xlabel="x", ylabel="y", title="Pathfinder Posterior Predictive");

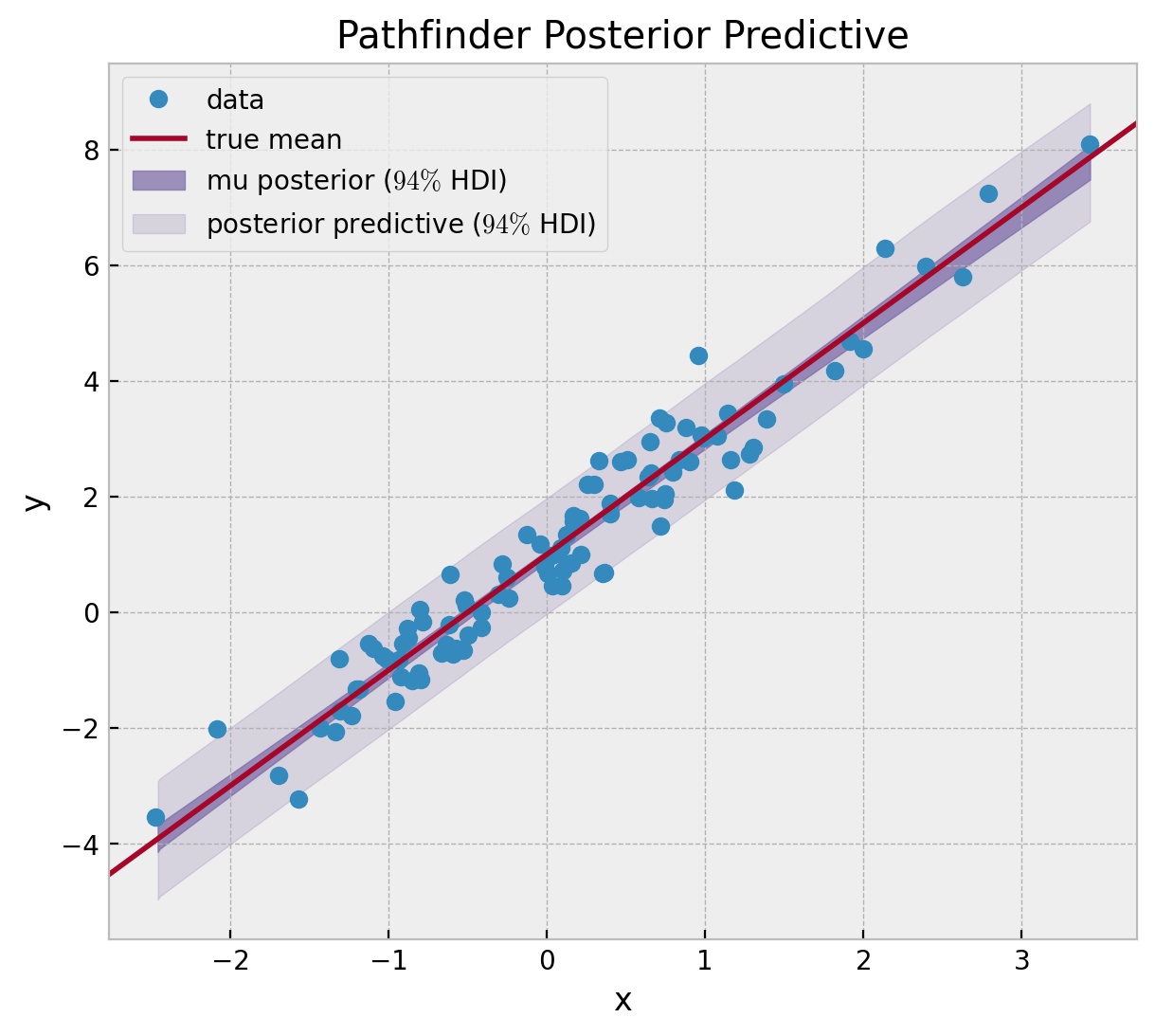
结果看起来不错！

FlowMC 正则化流采样器

我们可以像上面一样运行 FlowMC 采样器。我们只需要将对数密度函数适配到 FlowMC 格式即可。

定义对数密度函数

def logdensity_fn_flowmc(position, data):
    """FlowMC log-density function requires the position to be an array of shape
    (n_chains, n_dim) and the data to be a dictionary."""
    x = data["x"]
    y = data["y"]
    dict_position = dict(zip(param_info.z.keys(), position[..., None]))
    func = potential_fn(x, y)
    return -func(dict_position)

让我们验证对数密度函数是否正常工作。

n_dim = 3  # number of parameters
n_chains = 20  # number of chains

data = {"x": x, "y": y}
rng_key, subkey = random.split(rng_key)
initial_position_array = jax.random.normal(subkey, shape=(n_chains, n_dim))

logdensity_fn_flowmc(initial_position_array, data)

Array(-868.2817303, dtype=float64)

定义 FlowMC 采样器

我们现在可以定义 FlowMC 采样器。有关更多详细信息，请参阅文档中的此示例。

# local sampler: Metropolis-adjusted Langevin algorithm sampler class builiding the mala_sampler method
mala_sampler = MALA(logpdf=logdensity_fn_flowmc, jit=True, step_size=0.1)

rng_key, subkey = random.split(rng_key)
# nortmalizing flow model: Rational quadratic spline normalizing flow model using distrax.
nf_model = MaskedCouplingRQSpline(
    n_features=n_dim, n_layers=4, hidden_size=[32, 32], num_bins=8, key=subkey
)

%%time

sampler_params = {
    "n_loop_training": 7,
    "n_loop_production": 7,
    "n_local_steps": 150,
    "n_global_steps": 100,
    "learning_rate": 0.001,
    "momentum": 0.9,
    "num_epochs": 30,
    "batch_size": 10_000,
    "use_global": True,
}


rng_key, rng_subkey = random.split(rng_key)
nf_sampler = Sampler(
    n_dim=n_dim,
    rng_key=rng_subkey,
    data=data,
    local_sampler=mala_sampler,
    nf_model=nf_model,
    **sampler_params,
)

nf_sampler.sample(initial_position_array, data)

rng_key, subkey = jax.random.split(rng_key)
nf_samples = nf_sampler.sample_flow(subkey, 5_000)

['n_dim', 'n_chains', 'n_local_steps', 'n_global_steps', 'n_loop', 'output_thinning', 'verbose']

Global Tuning:   0%|          | 0/7 [00:00<?, ?it/s]

Compiling MALA body

Global Tuning: 100%|██████████| 7/7 [00:45<00:00,  6.57s/it]
Global Sampling: 100%|██████████| 7/7 [00:00<00:00, 13.46it/s]

CPU times: user 2min 44s, sys: 5min 15s, total: 7min 59s
Wall time: 47.2 s

可视化结果

我们收集后验样本并可视化结果。

posterior_samples_flowmc = dict(zip(param_info.z.keys(), nf_samples.T))

flowmc_idata = az.from_dict(posterior=posterior_samples_flowmc)

axes = az.plot_trace(
    data=flowmc_idata,
    compact=True,
    figsize=(10, 6),
    backend_kwargs={"layout": "constrained"},
)
plt.gcf().suptitle(
    t="FlowMC Trace - Transformed Space", fontsize=18, fontweight="bold"
);

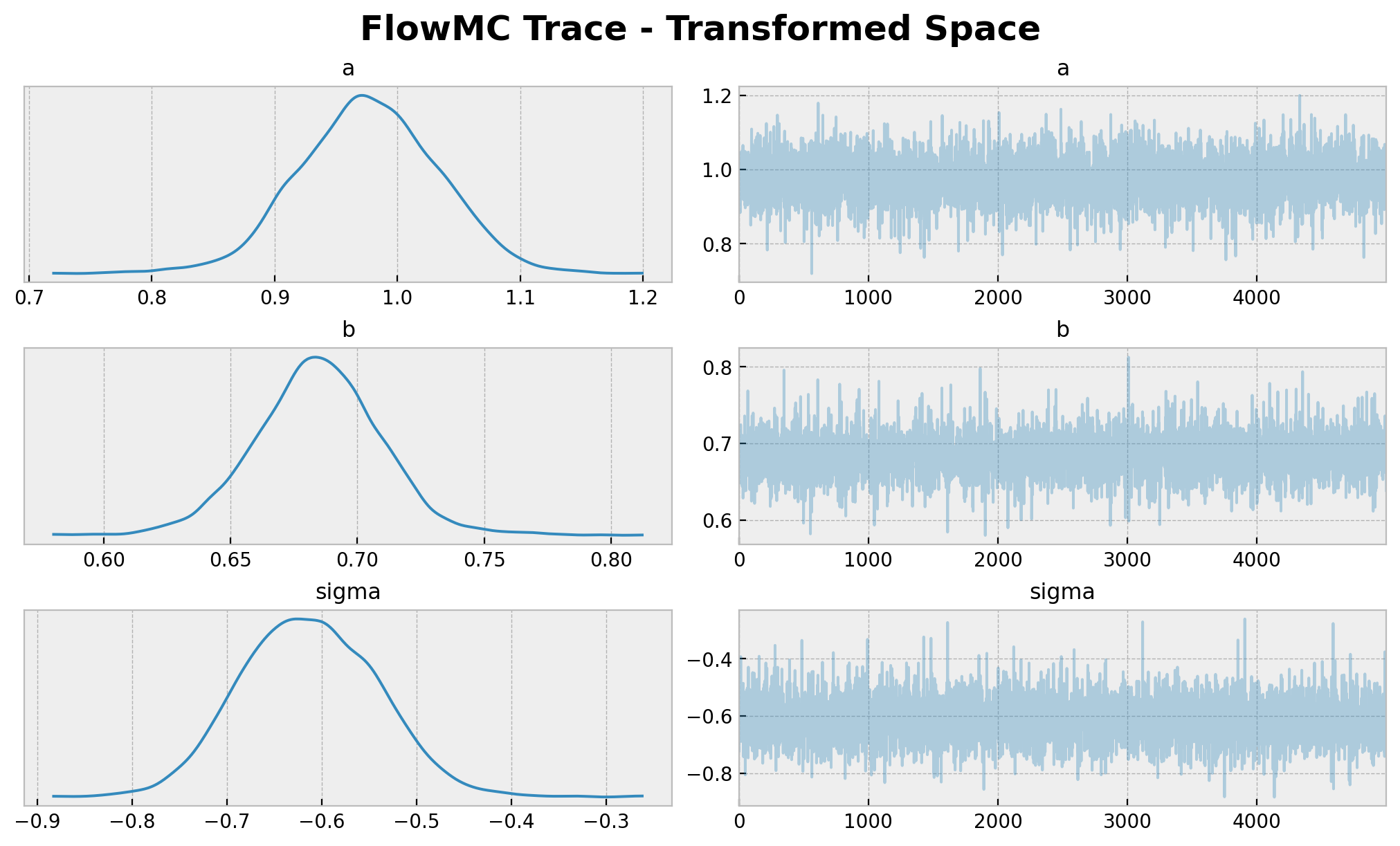
转换样本

我们将样本转换回原始空间，就像对 Pathfinder 所做的那样。

# posterior samples
posterior_samples_flowmc_transformed = jax.vmap(postprocess_fn(x, y))(
    posterior_samples_flowmc
)

# posterior predictive samples
rng_key, rng_subkey = random.split(rng_key)
posterior_predictive_samples_flowmc_transformed = Predictive(
    model=model, posterior_samples=posterior_samples_flowmc_transformed
)(rng_subkey, x)

idata_flowmc_transformed = az.from_dict(
    posterior={
        k: np.expand_dims(a=np.asarray(v), axis=0)
        for k, v in posterior_samples_flowmc_transformed.items()
    },
    posterior_predictive={
        k: np.expand_dims(a=np.asarray(v), axis=0)
        for k, v in posterior_predictive_samples_flowmc_transformed.items()
    },
)

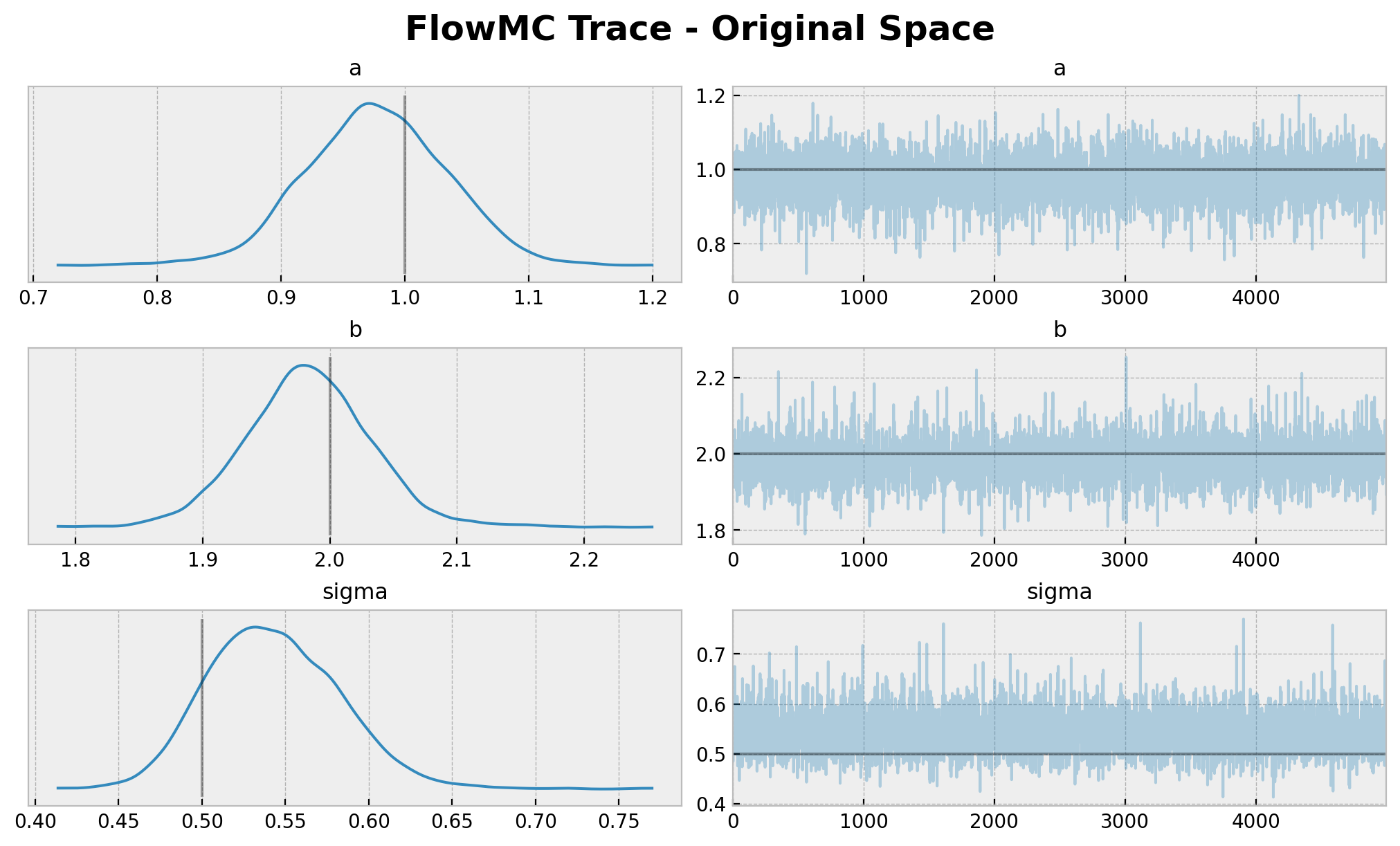
axes = az.plot_trace(
    data=idata_flowmc_transformed,
    var_names=["~mu"],
    compact=True,
    figsize=(10, 6),
    lines=[
        ("a", {}, a),
        ("b", {}, b),
        ("sigma", {}, sigma),
    ],
    backend_kwargs={"layout": "constrained"},
)
plt.gcf().suptitle(t="FlowMC Trace - Original Space", fontsize=18, fontweight="bold");

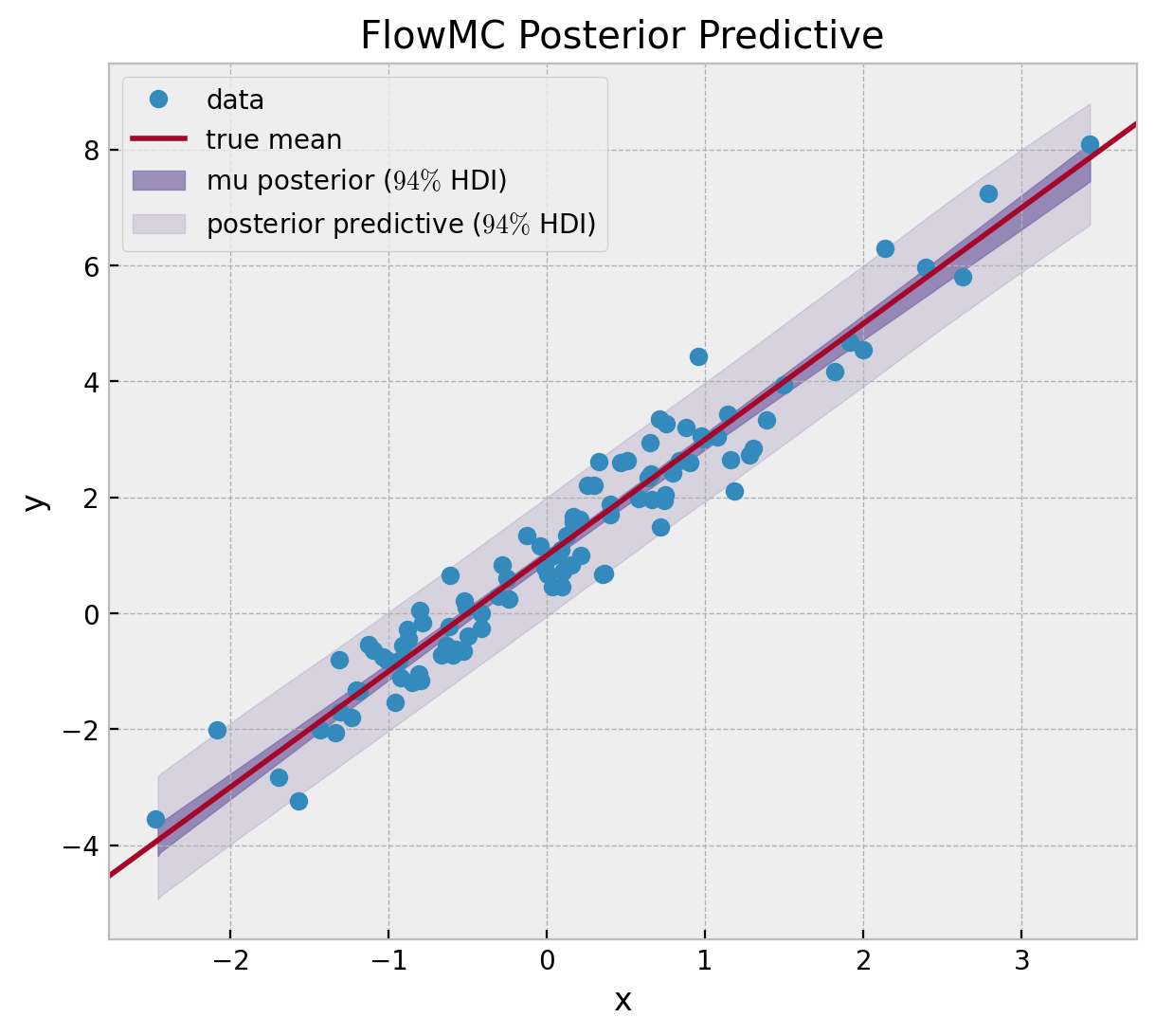
fig, ax = plt.subplots(figsize=(7, 6))
ax.plot(x, y, "o", c="C0", label="data")
ax.axline((0, a), slope=b, color="C1", label="true mean")
az.plot_hdi(
    x=x,
    y=idata_flowmc_transformed["posterior_predictive"]["mu"],
    color="C2",
    fill_kwargs={"alpha": 0.7, "label": "mu posterior ($94\\%$ HDI)"},
    ax=ax,
)
az.plot_hdi(
    x=x,
    y=idata_flowmc_transformed["posterior_predictive"]["likelihood"],
    color="C2",
    fill_kwargs={"alpha": 0.2, "label": "posterior predictive ($94\\%$ HDI)"},
    ax=ax,
)
ax.legend(loc="upper left")
ax.set(xlabel="x", ylabel="y", title="FlowMC Posterior Predictive");

模型比较

最后，我们比较两种采样器的结果。

az.plot_forest(
    data=[idata_pathfinder_transformed, idata_flowmc_transformed],
    model_names=["Pathfinder", "FlowMC"],
    var_names=["a", "b", "sigma"],
    combined=True,
    figsize=(8, 5),
    backend_kwargs={"layout": "constrained"},
);

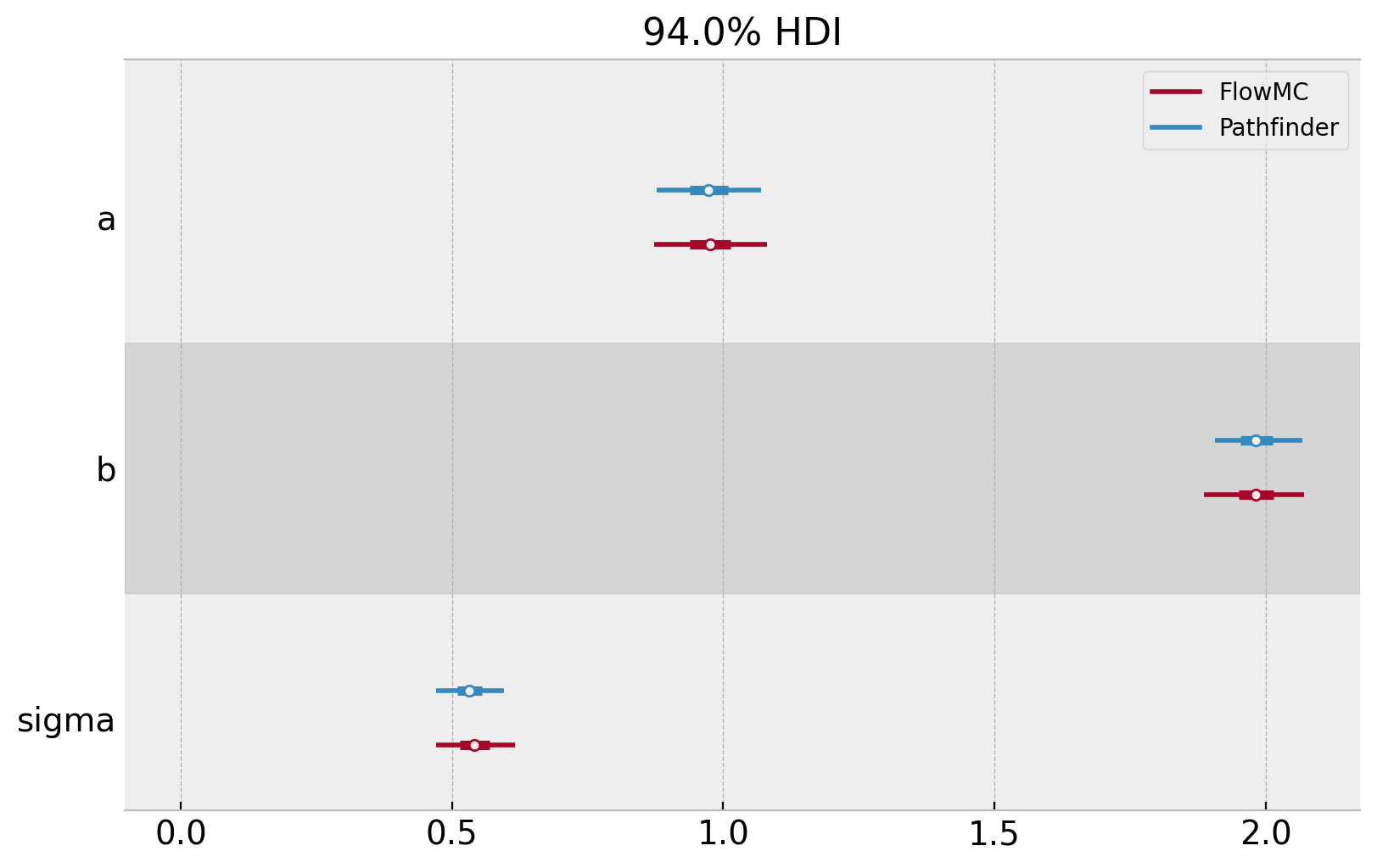
两种采样器都表现良好，结果非常相似。

注意： 我们想提一个有助于使用其他推断算法拟合 NumPyro 模型的相关项目

bayeux 让您可以使用 JAX 编写概率模型，并立即获得最先进的推断方法的访问权限。API 旨在简单、自解释且有用。只需提供一个对数密度函数（甚至不需要归一化），以及一个该对数密度有限的单点（指定为 pytree）。然后让 bayeux 完成其余的工作！

快来试试吧！