示例：捕食者-猎物模型

本示例复现了出色的案例研究 [1]，该研究利用 Lotka-Volterra 方程 [2] 描述了加拿大猞猁（捕食者）和雪鞋兔（猎物）种群的动态。我们将使用从 [3] 获取的数据集，并运行 MCMC 来推断控制动态的微分方程的参数。

参考文献

1. Bob Carpenter (2018), “捕食者-猎物种群动态：Stan 中的 Lotka-Volterra 模型”。

2. https://en.wikipedia.org/wiki/Lotka-Volterra_equations

3. http://people.whitman.edu/~hundledr/courses/M250F03/M250.html

import argparse
import os

import matplotlib
import matplotlib.pyplot as plt

from jax.experimental.ode import odeint
import jax.numpy as jnp
from jax.random import PRNGKey

import numpyro
import numpyro.distributions as dist
from numpyro.examples.datasets import LYNXHARE, load_dataset
from numpyro.infer import MCMC, NUTS, Predictive

matplotlib.use("Agg")  # noqa: E402


def dz_dt(z, t, theta):
    """
    Lotka–Volterra equations. Real positive parameters `alpha`, `beta`, `gamma`, `delta`
    describes the interaction of two species.
    """
    u = z[0]
    v = z[1]
    alpha, beta, gamma, delta = (
        theta[..., 0],
        theta[..., 1],
        theta[..., 2],
        theta[..., 3],
    )
    du_dt = (alpha - beta * v) * u
    dv_dt = (-gamma + delta * u) * v
    return jnp.stack([du_dt, dv_dt])


def model(N, y=None):
    """
    :param int N: number of measurement times
    :param numpy.ndarray y: measured populations with shape (N, 2)
    """
    # initial population
    z_init = numpyro.sample("z_init", dist.LogNormal(jnp.log(10), 1).expand([2]))
    # measurement times
    ts = jnp.arange(float(N))
    # parameters alpha, beta, gamma, delta of dz_dt
    theta = numpyro.sample(
        "theta",
        dist.TruncatedNormal(
            low=0.0,
            loc=jnp.array([1.0, 0.05, 1.0, 0.05]),
            scale=jnp.array([0.5, 0.05, 0.5, 0.05]),
        ),
    )
    # integrate dz/dt, the result will have shape N x 2
    z = odeint(dz_dt, z_init, ts, theta, rtol=1e-6, atol=1e-5, mxstep=1000)
    # measurement errors
    sigma = numpyro.sample("sigma", dist.LogNormal(-1, 1).expand([2]))
    # measured populations
    numpyro.sample("y", dist.LogNormal(jnp.log(z), sigma), obs=y)


def main(args):
    _, fetch = load_dataset(LYNXHARE, shuffle=False)
    year, data = fetch()  # data is in hare -> lynx order

    # use dense_mass for better mixing rate
    mcmc = MCMC(
        NUTS(model, dense_mass=True),
        num_warmup=args.num_warmup,
        num_samples=args.num_samples,
        num_chains=args.num_chains,
        progress_bar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
    )
    mcmc.run(PRNGKey(1), N=data.shape[0], y=data)
    mcmc.print_summary()

    # predict populations
    pop_pred = Predictive(model, mcmc.get_samples())(PRNGKey(2), data.shape[0])["y"]
    mu = jnp.mean(pop_pred, 0)
    pi = jnp.percentile(pop_pred, jnp.array([10, 90]), 0)
    plt.figure(figsize=(8, 6), constrained_layout=True)
    plt.plot(year, data[:, 0], "ko", mfc="none", ms=4, label="true hare", alpha=0.67)
    plt.plot(year, data[:, 1], "bx", label="true lynx")
    plt.plot(year, mu[:, 0], "k-.", label="pred hare", lw=1, alpha=0.67)
    plt.plot(year, mu[:, 1], "b--", label="pred lynx")
    plt.fill_between(year, pi[0, :, 0], pi[1, :, 0], color="k", alpha=0.2)
    plt.fill_between(year, pi[0, :, 1], pi[1, :, 1], color="b", alpha=0.3)
    plt.gca().set(ylim=(0, 160), xlabel="year", ylabel="population (in thousands)")
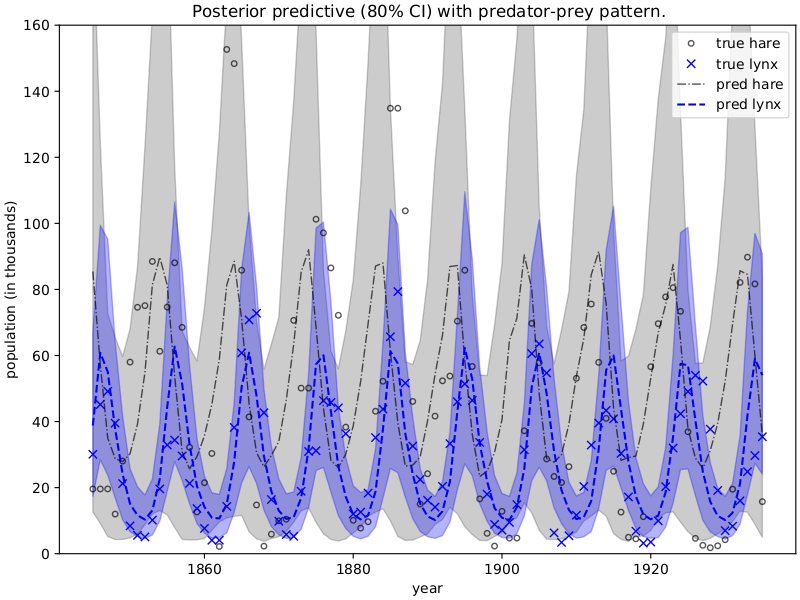
    plt.title("Posterior predictive (80% CI) with predator-prey pattern.")
    plt.legend()

    plt.savefig("ode_plot.pdf")


if __name__ == "__main__":
    assert numpyro.__version__.startswith("0.18.0")
    parser = argparse.ArgumentParser(description="Predator-Prey Model")
    parser.add_argument("-n", "--num-samples", nargs="?", default=1000, type=int)
    parser.add_argument("--num-warmup", nargs="?", default=1000, type=int)
    parser.add_argument("--num-chains", nargs="?", default=1, type=int)
    parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
    args = parser.parse_args()

    numpyro.set_platform(args.device)
    numpyro.set_host_device_count(args.num_chains)

    main(args)